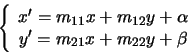rid2

Consideriamo ora l'applicazione affine

$\begin{displaymath} \left\{ \begin{array}{c} x'=m_{11}x+m_{12}y+\alpha \\ y'=m_{21}x+m_{22}y+\beta \end{array} \right. \end{displaymath}$

(4)

che in forma matriciale si scrive

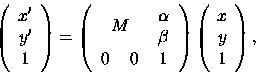$\begin{displaymath} \left( \begin{array}{c} x'\\ y'\\ 1 \end{array} \right)... ...ht)\left( \begin{array}{c} x\\ y\\ 1 \end{array} \right), \end{displaymath}$

(5)

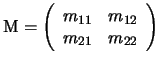dove $\mathrm M=\left( \begin{array}{cc} m_{11} & m_{12}\\ m_{21} & m_{22} \end{array} \right)$ è una matrice a coefficienti reali, invertibile; $\alpha,\beta\in \mathbf R$ .
La trasformazione inversa è:

$\begin{displaymath} \left( \begin{array}{c} x\\ y\\ 1 \end{array} \right)= ... ...)\left( \begin{array}{c} x'\\ y'\\ 1 \end{array} \right), \end{displaymath}$

(6)

dove $\mathrm P=\mathrm M^{-1}$ .

Ora, tenuto conto che

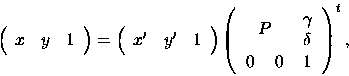
$\begin{displaymath}\left( \begin{array}{ccc} x & y & 1 \\ \end{array} \righ... ...$} &$\delta$ \\ 0\quad\,0&1 \\ \end{tabular} \right)^t,\end{displaymath}$

(la lettera in alto a destra sulla matrice è una t e sta ad indicare la trasposta della matrice in questione)

sostituendo () in (), otteniamo:

$\begin{displaymath} \left( \begin{array}{ccc} x' & y' & 1 \end{array} \righ... ...left( \begin{array}{c} x'\\ y'\\ 1 \end{array} \right)=0. \end{displaymath}$

(7)