DEFINIZIONE 5:

Sia A un anello commutativo. Un elemento a di A si dice invertibile (oppure un’ unità) se:

esiste b appartenente ad A tale che ab = 1.

---

Proposizione 2:

In un anello commutativo un elemento invertibile non è un divisore dello zero.

Osserviamo che se un elemento a di A è invertibile, e quindi se esiste b in A tale che ab = 1, tale b è unico.

Infatti se ab = 1 = ab¹ allora b =b¹.

Tale b è detto inverso e si denota con a^-1.

Se due elementi a e b di un anello commutativo A sono invertibili allora anche il loro prodotto lo è e:

(ab)^-1 = a^-1b^-1.

Questo si vede dal fatto che aba^-1b^-1= aa^-1bb^-1=1.

Per induzione su n vediamo che se n Z⁺ ed a è invertibile allora aⁿ è invertibile e si ha:

(aⁿ) ^-1 = (a^-1)ⁿ.

A questo punto possiamo definire aⁿ per qualsiasi intero n; cioè:

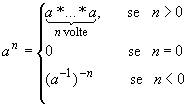Valgono le solite regole di calcolo per gli esponenti.