ACHILLE E LA
Parte I
Da Zenone di Elea a Giordano Bruno
INDICE:
0. Introduzione.5. Aggirare l'infinito: il metodo di Esaustione.
7. Dio e l'infinito in atto: il medioevo cristiano.
Achille e la Tartaruga sono i protagonisti di
quello che forse è il più famoso tra i paradossi
matematici: noi lo prenderemo come punto di partenza per esplorare il
modo in cui il concetto di infinito sia intervenuto in matematica
a partire dalla mondo greco
classico, caratterizzato da un Horror
infiniti che portò a cercare di eliminare il
più possibile l'uso di questo concetto all'interno del discorso
matematico.
Il paradosso di Achille e la Tartaruga, del filosofo Zenone di Elea (circa 500 a.C.), ci è giunto nella descrizione fattane da Aristotele (384-322 a.C.) nella Fisica:
"Il secondo argomento è quello detto di Achille. Eccolo: il più lento corridore non sarà mai raggiunto nella sua corsa dal più veloce. Infatti sarà necessario che l'inseguitore proceda fin là donde si è mosso il fuggitivo, quindi è necessario che il corridore più lento si trovi sempre un po' più innanzi".L'argomento si può esprimere in questi termini: supponiamo che si svolga una singolare gara di corsa fra il Pelide Achille (il piè veloce) ed una tartaruga. La sfida è impari, ma la tartaruga parte con un po' di vantaggio, per esempio 10m
Fig.1
Nel tempo che Achille impiega per andare da A
0, il suo punto di partenza, a T0=A
1 , il punto da cui parte la tartaruga, quest'ultima si
sarà spostata in una posizione T1 (vedi
ancora Fig. 1), e quando Achille arriva in T1=A2,
la tartaruga avrà raggiunto una nuova posizione in T2
.
Altrettanto accade per T3, T
4 ,... e via all'infinito. Quindi il paradosso sta qui:
Achille non raggiungerà mai la tartaruga!
Per farlo dovrebbe percorrere un infinità di tratti del tipo Tn - Tn +1, sempre più piccoli, ma mai nulli.
Vediamo di analizzare meglio il paradosso
utilizzando dei dati numerici per le velocità dei due
contendenti:
Allora Achille impiegherà un secondo per
portarsi in T0, ed in quel tempo la tartaruga
percorrerà un metro (cioè la distanza T0-T1
) è un metro. Poi Achille impiega 0,1 secondi per arrivare
in T1, mentre la tartaruga percorre 0,1 metri
arrivando in T2.
La situazione ai passi successivi è
esemplificata dalla seguente tabella:
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
Se vogliamo sapere dopo quale distanza Achille
raggiungerà la tartaruga, dovremo sommare tutti i termini ( infiniti !) che appaiono nella terza colonna,
ottenendo così :
|
|
una distanza finita quindi, anche se ottenuta sommando infiniti addendi.
Ugualmente se vogliamo sapere dopo quanto tempo Achille
raggiunge la tartaruga, sommeremo i termini che appaiono nella seconda
colonna, ottenendo (in secondi):
|
|
Il tempo impiegato non è quindi infinito,
ma poco più di un secondo!
Cos'è che viene evidenziato in tutto questo ragionamento? Che è concepibile il seguente fatto:
Una somma di infiniti addendi non nulli può anche dare un totale finito.
In questo modo, appare, abbiamo facilmente risolto il
paradosso proposto da Zenone....
Non del tutto; questo modo di risolvere il paradosso
rischia infatti di banalizzarlo, nascondendo molte cose, vediamolo
meglio:
* Innanzi tutto
la scelta fatta per i valori numerici delle velocità e
degli spazi percorsi rende molto facile il vedere intuitivamente qual
è
il risultato della somma: con valori diversi non sarebbe affatto
semplice vedere immediatamente che il risultato non è
infinito.
* Bisogna anche considerare che il nostro sistema di scrivere i numeri (cioè il sistema posizionale decimale ed il rappresentare i decimali infiniti periodici) ci rende le cose molto più semplici e intuitive in questo caso, mentre gli antichi sistemi come quello greco (ove i numeri venivano indicati con lettere: alfa = 1, beta = 2 e così via) o anche quello romano rendono i calcoli molto meno immediati e la soluzione non così intuitibile.
* Ma c'è un
altro problema, ben più sostanziale:
|
|
Il significato della somma di due o più numeri è chiaro, si tratta di un'operazione ben definita, ma sommare infiniti numeri è invece una operazione che per avere un sen so richiede una definizione molto più complessa (nel nostro esempio questa complessità è celata dall'uso di numeri particolarmente semplici).
Quella di somma infinita (che nel linguaggio matematico odierno è detta serie ) è un'operazione per la quale una definizione di un certo rigore apparirà solo verso il 1700 (e quella attualmente in uso solo nell'800), quindi ben più di 2000 anni dopo che Zenone ebbe segnalato con il suo paradosso la difficoltà di questo concetto.
Per evidenziare quanto problematico sia il
concetto di somma infinita consideriamo un altro esempio,
apparentemente analogo, e cioè quello della seguente somma
(infinita):
|
|
Il matematico Guido Grandi (1671-1742), professore all'università di Pisa, osserverà il seguente paradosso, dovuto al raggruppare gli addendi in modo diverso:
|
|
|
|
Quindi il risultato della somma è sia 0 che 1 !
Si vede quindi che quando si cerca di estendere alle quantità infinite il nostro modo usuale di operare con le quantità finite c'è la necessità di definire nuove regole e procedimenti, se non si vuole cadere in contraddizioni o formule prive di senso.
Le considerazioni precedenti ci indicano che Zenone con questo paradosso (e con gli altri di cui parleremo più avanti) aveva "messo il dito nella piaga": aveva segnalato la difficoltà di essere rigorosi nei ragionamenti riguardanti l'infinito, mostrando come anche nozioni di uso comune (principalmente quelle riguardanti il movimento) potessero, quando analizzate da vicino, racchiudere una grande complessità e come la loro matematizzazione fosse un'opera molto ardua.
Purtroppo non ci è noto quale fosse il
bersaglio più diretto dei paradossi Zenoniani, essendoci stati
tramandati "di seconda mano" (attraverso la loro confutazione fatta da
Aristotele); la congettura più comune è che essi fossero
principalmente in polemica con la scuola pitagorica e con l'atomismo
che era già entrato
in crisi. Dedicheremo quindi la nostra attenzione a questa scuola prima
di
continuare nella esposizione degli altri paradossi.
Pitagora nacque nell'isola di Samo intorno al 580 a.C. e la sua figura è circondata da un alone di leggenda che ce lo mostra nella veste di "santone", oltre che come matematico e filosofo.
Fu attivo principalmente nell'Italia Meridionale (Crotone) dove fondò una confraternita di tipo quasi monacale che gli sopravvisse per circa due secoli. Di lui si dissero le cose più disparate (che aveva compiuto miracoli, che era figlio di Apollo) specialmente ad opera del movimento neo-pitagorico fiorito nel periodo alessandrino, anche se alcune leggende sono già presenti in Aristotele.
L'idea-forza dei Pitagorici si può (ma banalizzando molto) riportare a questa:
"il numero è il principio di tutte le cose".
Questo concetto è legato ad una visione sostanzialmente atomista della natura: ogni cosa è formata da un numero finito (magari molto grande) di enti (atomi) piccolissimi e non visibili, legati fra loro con varie configurazioni geometriche ed immersi in uno spazio vuoto.
Si addiveniva così ad un'idea molto geometrica (quasi fisica) di numero, e le leggi riguardanti i numeri venivano ritenute leggi fondamentali della natura.
Questo modo di vedere aveva portato a dei buoni risultati in geometria ed in teoria dei numeri, le quali vennero sviluppate insieme in una aritmo-geometria che visualizzava e rendeva facilmente intuibili le proprietà numeriche e geometriche.
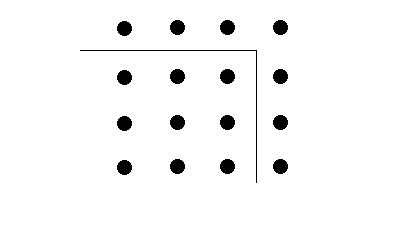
ove ogni numero dispari (qui il numero 7
) è visto come uno gnomone (= "squadra", cioè i
sette punti che compongono la prima riga e ultima colonna ) che
è esattamente la differenza di due quadrati
(nell'esempio 16 - 9 = 7
); se si vuole vedere una semplice descrizione algebrica di questo
fatto, cliccare QUI .
Poiché ogni grandezza (linee, superfici, volumi) veniva pensata come costituita da un numero finito (per quanto grande) di atomi, ogni rapporto fra grandezze doveva essere esprimibile come quoziente di due numeri interi, e quindi con i soli numeri interi (ed i loro rapporti) si doveva poter "misurare" tutto il reale.
Questa visione (ironicamente, proprio grazie al
Teorema di Pitagora) si doveva scontrare con la scoperta delle
grandezze incommensurabili, che la contraddiceva completamente.
La scoperta che il rapporto fra la lunghezza della diagonale
di un quadrato ed il suo lato non
è esprimibile tramite il rapporto di due numeri interi è
uno di quei passi che sono stati fondamentali nella storia della
scienza (anche se adesso è materia da scuola media inferiore),
per vedere la sua breve ed elegante dimostrazione cliccare QUI .
La scoperta dell'incommensurabilità fra la diagonale e il lato di un quadrato metteva in crisi i fondamenti stessi della dottrina pitagorica: i numeri non bastavano a descrivere la realtà !
Un primo effetto di tale crisi fu il fatto che la matematica greca si concentrò soprattutto sulla geometria, nella quale raggiunse grandi vette di approfondimento e di sistemazione logica, come negli Elementi di Euclide (325? a.C.- 265 ? a.C.), il libro più ristampato al mondo dopo la Bibbia, mentre la manipolazione puramente numerica (anche per la mancanza di un sistema simbolico efficiente) fu meno sviluppata, e soprattutto meno trattata come un settore indipendente della matematica, mentre si affidò molto alla possibilità di rappresentazioni geometriche.
Il filosofo che fu il maggior sostenitore del modello
atomistico è senza dubbio
Democrito di Abdera (460? a.C.-360?a.C.) che fu anche un
matematico; sono citati da autori
a lui posteriori suoi testi dal titolo: Sui numeri , Sulla
geometria
, Sulle tangenti, Sugli irrazionali; ma nulla di questi
trattati è arrivato fino a noi. Quel poco che sappiamo delle sue
idee in matematica ci arriva attraverso le citazioni fatte da autori
sucessivi,
ad esempio Archimede (vedi sezione 5) dice che Democrito fu il primo ad
enunciare il teorema che afferma che il volume di un cono è un
terzo
di quello di un cilindro di uguale altezza, e che quello di una
piramide
è un terzo di quello di un prisma di uguale altezza. La
cosa
per noi interessante è che Democrito lo faccia usando metodi
"infinitesimali"
(vedi Fig. 7).
Plutarco ci informa di un paradosso attribuito a
Democrito anch'esso riguardante problemi di "infinitesimi":
Se un cono fosse tagliato con piani paralleli alla sua base [infinitamente vicini alla base stessa], cosa dobbiamo pensare delle superfici che formano le sezioni ottenute? Sono uguali fra loro o no? Perché se sono disuguali, allora rendono il cono irregolare, indentato, come a gradini, e non liscio; ma, se sono uguali, allora il cono avrebe la proprietà del cilindindro e sarebbe formato da sezioni circolari uguali e non diverse, il che è assurdo.Ci sono aspetti importanti in questo paradosso e quello che per noi è più interessante è che Democrito pensa un solido come composto dalle sue (infinite) sezioni piane, e (come ci dice Archimede) può aver usato questa idea per dimostrare uguaglianze fra volumi di solidi diversi, anche se l'enunciare questo paradosso pare mostrare che già Democrito stesso cogliesse gli aspetti problematici di questo tipo di procedure (la somma di infiniti triangoli di volume zero non ha volume zero?).
Non sappiamo se Democrito (o altri della sua scuola) abbiamo tentato delle risposte a questi problemi, sappiamo che tali difficoltà ebbero come effetto una crisi che portò alla necessità di reimpostare il problema di quale fosse la natura delle grandezze geometriche (e fisiche): una volta crollata l'ipotesi pitagorica che le grandezze fossero formate da un numero finito di enti indivisibili, si dovette guardare agli enti geometrici come continui, divisibili all'infinito in parti più piccole con un processo che non ha mai termine, oppure (o allo stesso tempo) come enti discreti, cioè composti di elementi indivisibili fondamentali che però, dopo la scoperta dell'incommensurabilità, dovevano apparire in numero infinito anche nel formare grandezze di misura finita.
Come si vede, in entrambi concetti siamo costretti a far intervenire l'idea di infinito: come infinita divisibilità nel primo caso, come infinito numero degli indivisibili (atomi, monadi o punti, come verranno chiamati) che formano gli enti geometrici e fisici, ed anche nel concetto di infinitesimo che ad essi si verrebbe ad attribuire.
Entrambe le visioni presentano vari ordini di
problemi, come vedremo nella prossima sezione, ed una visione
soddisfacentemente rigorosa di tutto ciò sarà messa a
punto solo nel secolo scorso, con la nascita del concetto di limite .
Che un'analisi rigorosa del continuo e del discreto portasse a scoprire la difficoltà di una sistemazione logica di tali concetti è mostrato dai paradossi con i quali Zenone li attaccò. Contro il tentativo di salvare l'atomismo geometrico dei pitagorici, egli osservò (nel paradosso detto dei Molti) che se gli "atomi" non hanno grandezza (dimensione, estensione, lunghezza, volume), e cioè se hanno grandezza zero, allora per quanti se ne sommino avremo sempre grandezza zero, quindi non potrebbe esistere nulla di misura diversa da zero.
Se invece gli atomi hanno estensione non nulla, arriviamo ugualmente ad una contraddizione: ogni grandezza deve essere formata da un numero infinito di atomi (poiché la scoperta della incommensurabilità ha mostrato che supporre le grandezze formate da un numero finito di atomi porta a contraddizione), ma un numero infinito di grandezze finite non nulle mi darebbe una grandezza infinita, e quindi tutte le grandezze dovrebbero essere infinite. Perciò entrambe le ipotesi portano ad una contraddizione.
Gli altri paradossi riguardano il moto e le due ipotesi sulla natura del tempo e dello spazio (come l' Achille di cui abbiamo già parlato): quella "atomica" e quella di infinita divisibilità.
La Dicotomia è un argomento analogo all'Achille, ed è anch'esso basato sulla infinita divisibilità: si afferma che il moto è impossibile in quanto un corpo per andare da A ad B dovrebbe prima percorrere la metà di quella distanza, e prima ancora un quarto, e un ottavo, e così via. Quindi esso dovrebbe percorrere infiniti tratti non nulli e per farlo impiegherebbe un tempo infinito.
Se invece noi supponiamo che il tempo e lo spazio non
siano infinitamente suddivisibili, ma composti di "atomi" indivisibili,
che chiameremo rispettivamente "istante" per il tempo ed "intervallo"
per lo spazio, non ci salveremo ugualmente dall'implacabile Zenone.
Nel paradosso detto dello Stadio egli scova una
contraddizione anche in questa ipotesi: consideriamo tre segmenti
uguali che si trovano nella seguente posizione:

Un ultimo paradosso (ancora contro la suddivisione del tempo in istanti) concerne l'idea stessa di moto, ed è quello della Freccia: se io guardo una freccia in volo in un dato istante, quella occupa una certa posizione determinata, ed è quindi indistinguibile da una freccia che in quell'istante sia ferma in quella posizione. Allora la freccia non si muove, o, per dirla con un'altra formulazione (come viene riportato da Aristotele in Fisica VI):
Ogni cosa che occupa uno spazio uguale a se stessa (in uno ed un sol posto) è in stato di quiete, ma questo è vero per la freccia in ogni istante del suo volo. Quindi la freccia non si muove.Questo paradosso coinvolge la nozione di velocità istantanea ed il significato stesso di "essere in movimento" (cfr. §4).
Notiamo che alcuni commentatori hanno teso a
presentare i paradossi di Zenone come puri sofismi, tesi solo a
confondere
gli avversari, o comunque come argomenti "paralizzanti" che hanno
inibito
l'analisi di ciò di cui trattavano (ad esempio il Bell, in [ Be ]); al contrario la loro estrema
utilità è
stata di mettere bene in luce i problemi di una trattazione rigorosa
dei
concetti che coinvolgono l'infinito e l'infinitesimo, con i quali i
matematici
avranno a che fare per secoli prima di ottenerne una sistemazione
soddisfacente.
Degli effetti di questa crisi della visione pitagorica
abbiamo già detto (con questa "scissione" avvenuta fra geometria
e aritmetica) ma un'altra divisione si va creando in questo periodo, ed
è quella fra matematica e realtà fisica, che avviene con
i tardo-pitagorici e soprattutto con la scuola platonica, la prima ad
esprimere con chiarezza la distinzione fra l'astrazione dei concetti
geometrici e la concretezza degli oggetti fisici.
Ad esempio, a proposito dei matematici, Platone
(427-347 a.C.) scrive nella Repubblica (Libro VI):
"... sebbene essi facciano anche uso delle forme visibili e vi ragionino intorno, non è ad esse a cui pensano, ma alle idee a cui assomigliano".Non è noto quanto Platone abbia personalmente contribuito alla matematica del suo tempo; quello che è certo è che la centralità che egli dava allo studio della matematica, e l'insistenza sulla necessità di dimostrazioni deduttive (rispetto a metodi induttivi o sperimentali) sono state un fattore importante nell'indirizzare la matematica greca sulla strada del rigore formale e che l'Accademia platonica divenne il più importante centro matematico del mondo greco nel IV secolo a.C.
È con Aristotele (il "Maestro di color che sanno") che si ha il più compiuto tentativo di "metter ordine" nell'uso dell'infinito in matematica (ed in fisica e metafisica); l'opinione di Aristotele sull'infinito rimarrà sostanzialmente quella prevalente fino al '600 (e per alcuni aspetti fino al secolo scorso).
Aristotele (vedi Fisica, III, 6 ) fa una chiara divisione fra
Ad esempio per Aristotele dire che i numeri sono
infiniti significa solo che, qualunque numero si pensi, se ne
può trovare
uno maggiore, ma solo i singoli numeri finiti sono pensabili, anche se
non
ne esiste " il più grande".
Aristotele respinge completamente la
possibilità che l'infinito in atto possa essere utilizzato in
matematica:
In realtà essi [i matematici] non hanno bisogno dell' infinito e non lo usano. Essi postulano [ad esempio] che la linea retta possa essere prolungata a piacere, tanto quanto si vuole...Per Aristotele è la possibilità di prolungare la retta che viene usata, non l'esistenza della "retta infinita": l'unica infinità ammessa è quella potenziale.
(Aristotele, Fisica, III, 7).
Notiamo che è con questa accezione che il concetto di retta è usato nella geometria greca (ad esempio in Euclide); nella geometria contemporanea si usa il termine retta per indicare un oggetto infinito; l'idea greca corrisponde di più a ciò che oggi si chiama segmento, considerato però prolungabile a piacere.
Può giovare ricordare che il termine usato allora per "infinito" è apeiron, che non ha proprio lo stesso significato del nostro "infinito", ma è più letteralmente traducibile con "illimitato" o "indefinito", e porta con sé un senso di "mancanza di forma" e di negatività, indeterminatezza che il nostro termine "infinito" non ha, contenendo invece anche un senso di compiutezza che è assente nel termine greco. Sempre nella Fisica (III,6), si legge:
"L'infinito non è ciò al di fuori di cui non c'è nulla, ma ciò al di fuori di cui c' è sempre qualcosa".L'infinito non è quindi un Assoluto: è qualcosa che per la sua illimitatezza non può essere concepito dal nostro pensiero nella sua totalità. Per questo rimane associata all' apeiron una valenza negativa: un senso di potenzialità non attuata e non attuabile né concepibile, ed anche un senso di indeterminatezza, di caoticità.
Questo Horror infiniti porta
all'esclusione di ogni infinito attuale (o anche infinitesimo attuale)
in matematica: in geometria le grandezze continue saranno
(potenzialmente)
divisibili all'infinito, senza che si possa mai giungere ad un termine
di
questo processo, e senza che esistano degli "indivisibili" ultimi, e
cioè
quegli atomi che avevano caratterizzato la visione pitagorica e che
erano
stati teorizzati anche da Senocrate, il successore di Platone a capo
dell'Accademia.
Aristotele dice esplicitamente che nessuna accumulazione di punti
può
generare una grandezza continua essendo i punti indivisibili, mentre la
caratteristica della continuità è proprio quella di
essere
infinitamente divisibile. In modo analogo è negata la
possibilità
che gli intervalli di tempo siano composti da "istanti".
Si approfondisce dunque la distanza fra il modo
di concepire il mondo dei numeri e quello della geometria:
le grandezze sono continue mentre i numeri sono discontinui ed incapaci
di rappresentare la continuità:
Il Numero è una pluralità di unità, una determinata quantità di esse. Quindi il numero si ferma [nella direzione della piccolezza] a ciò che è indivisibile [l'unità]... Invece nella direzione della grandezza è sempre possibile pensare un numero più grande... Quindi questo è un infinito potenziale,... non in atto, ma consistente in un processo di divenire, come il tempo.... Con le quantità [geometriche o fisiche] è vero il contrario. Ciò che è continuo è diviso all'infinito, mentre non c'è infinità nella direzione dell'incremento. Ogni grandezza che può essere raggiunta potenzialmente, lo può essere anche effettivamente.
( Aristotele, Fisica, IV).
Quindi, per Aristotele:
Le grandezze sono continue mentre i numeri sono discontinui (ed incapaci di rappresentare la continuità).Come si è visto, ci sono inoltre due possibilità per l'infinito potenziale:
| L'infinito nella direzione dell' accrescimento - Questo pertiene tipicamente al numero ed anche agli enti geometrici (rette, piani). .
|
| L'infinito nella direzione della divisibilità - Questo invece pertiene alle quantità della geometria e della fisica. .
|
Le quantità geometriche e fisiche non sono concepite come infinitamente accrescibili, nemmeno potenzialmente, perché anche l'Universo è pensato come finito e dotato di limite, quindi un infinito accrescimento di una grandezza sarebbe in contraddizione con tale visione.
Per descrivere come Aristotele affronti i paradossi
Zenoniani descritti nella sezione precedente (dando una sua
soluzione) dobbiamo considerare la sua Fisica, ove egli tratta
il
problema del movimento.
Schematicamente, nella Fisica, Aristotele tratta il problema del movimento dando una descrizione qualitativa di questo fenomeno: egli implicitamente respinge la possibilità di averne una trattazione quantitativa e matematica, coerentemente con l'idea che il numero (discreto) non possa descrivere un fenomeno come il moto che riguarda le grandezze (continue).
Secondo Aristotele i moti si dividono in violenti (o artificiali) e naturali.
A loro volta i moti naturali sono di due tipi: quello
circolare e quello rettilineo.
Di moto rettilineo, verso il basso o l'alto, si muovono
i quattro elementi costitutivi di ogni corpo (fuoco, terra, acqua e
aria), mentre i corpi celesti sono fatti di un quinto elemento (
l'etere o
quintessenza ).
Il fuoco e l'aria tendono sempre a muoversi verso l'alto (i Cieli), la terra e l'acqua verso il basso (la Terra).
L'idea è che il moto naturale è una tendenza di ogni corpo ad assumere "la posizione che gli compete"; cioè ad assumere in atto, effettivamente, ciò che esso è in potenza (Fis. III). Si tratta di una spiegazione teleologica , che analizza cioè il moto in base ad un suo fine, non alle sue cause: i corpi pesanti, lasciati a se stessi cadono verso la Terra perché composti di terra ed acqua che, per loro natura, tendono verso il basso, tendono ad assumere la posizione "che loro compete".
Per quanto riguarda invece i moti artificiali, per risolvere il problema del perché un corpo messo in moto (ad es. un proiettile) continui a muoversi anche quando non è più soggetto ad una forza, Aristotele sostiene che chi spinge il corpo è l'aria che lo circonda: scossa dal lancio essa continua a "richiudersi" dietro il corpo che si muove, sospingendolo (anche se con una forza sempre minore).
In base a questa idea Aristotele sostiene che un corpo non potrebbe muoversi nel vuoto (Fis. IV), anzi nega la possibilità stessa dell'esistenza del vuoto, in radicale polemica con la fisica atomista e meccanicista di Democrito, che vedeva il mondo come composto da atomi vaganti nel vuoto infinito (e che pare avesse anche intuito anche il principio di inerzia). Anche il moto naturale degli astri viene infatti concepito come svolgentesi nell' etere, non nel vuoto. Contro queste concezioni (e non solo contro la teoria eliocentrica) dovrà combattere a fondo Galileo nel fondare le teorie della dinamica moderna.
Per risolvere il paradosso della Freccia (ed
anche dello Stadio) Aristotele semplicemente nega che abbia
senso il concetto di "velocità di un corpo ad un dato istante":
Nulla può essere in moto nel presente... né può darsi che qualcosa sia in quiete nel presente.
(Aristotele, Fisica, VI)Quindi si può associare ad un corpo il concetto di essere in quiete od in moto solo osservandolo per un certo lasso di tempo: si esclude in questo modo la possibilità di definire quella "velocità istantanea" che sarà invece alla base della dinamica Newtoniana (cioè hanno senso solo le "velocità medie", tenute da un corpo in un certo lasso di tempo).
I paradossi della Dicotomia e dell'Achille
vengono invece risolti affermando che sebbene
sia vero che non è possibile attraversare uno spazio infinito in
un tempo finito, è sempre possibile attraversare in un tempo
finito
uno spazio finito, anche se esso è infinitamente suddivisibile (
Fis. VI, 2 e VI, 9).
In sostanza le risposte di Aristotele a Zenone (a
parte l'ultima di quelle descritte sopra) eludono le questioni
matematiche in essi racchiuse, spostando le questioni sul piano della
dialettica e rinunciando a priori ad una descrizione matematica dei
fenomeni in analisi.
5. Aggirare
l'infinito: le proporzioni di Euclide ed il metodo di Esaustione.
Con la messa al bando dell'uso dell'infinito e
degli infinitesimi, come con la scoperta di grandezze
incommensurabili si ponevano vari problemi in geometria, per
esempio nel determinare aree
di figure delimitate da linee curve o che cosa si intenda per
"rapporto"
fra grandezze incommensurabili. Vedremo come la matematica greca
riuscì a dare una risposta ad entrambe quest'ultime due
questioni tramite dei metodi ingegnosi che riuscirono ad "aggirare",
per così dire, l'uso dell'infinito (degli infinitesimi
soprattutto).
1° Problema: Il rapporto fra incommensurabili.
Come abbiamo visto i pi tagorici avevano già scoperto l'impossibilità di esprimere tutti i rapporti fra segmenti (in generale fra grandezze geometriche) tramite rapporti di numeri interi. Consideriamo ad esempio il seguente problema:
...Il passo V può essere espresso, in notazione contemporanea, così:
III. Ragione (o rapporto) è una relazione fra due grandezze omogenee, rispetto alla loro quantità.
IV. Si dice che le grandezze hanno ragione tra loro, quando ciascuna può essere multipla in modo da superare l'altra.
V. Si dice che la ragione di una prima grandezza ad una seconda è uguale a quella di una terza ad una quarta quando, presi degli equimultipli qualsiasi della prima e della terza, e degli equimultipli qualsiasi della seconda e della quarta, se il multiplo della prima è maggiore del multiplo della seconda, anche il multiplo della terza sia maggiore del multiplo della quarta; se uguale, uguale; se minore, minore.
...
Date quattro grandezze a ,b,c,d avremo che esse sono in proporzione quando, presi comunque due interi m, n, avremo chePer noi le tre implicazioni qui sopra sono esattamente equivalenti a dire che a:b=c:d (infatti equivalgono a dire che ogni frazione m/n è maggiore, uguale o minore di b/a se e solo se è maggiore, uguale o minore di d/c), ma in effetti permettono di definire il concetto di essere in rapporto, cioè la proporzionalità, senza usare il quoziente a:b , il quale, se a e b sono incommensurabili, non ha alcun senso aritmetico per un matematico dell'epoca (non è esprimibile come rapporto fra numeri).ma > nb implica mc > nd ,
ma < nb implica mc < nd ,
ma = nb implica mc = nd .
Notiamo anche il termine IV, che esclude la presenza di grandezze infinitesime o infinite una rispetto all'altra. Ad esempio, consideriamo, nello stesso testo degli Elementi , quello che può sembrare un infinitesimo "in atto": l'angolo curvilineo.
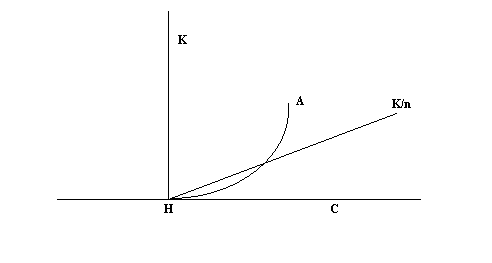
Indichiamo K = KHC l'angolo retto di Fig. 6; per quante volte, n, si sommi l'angolo CHA a se stesso, è impossibile superare l'angolo K, infatti se si avesse: n .CHA > K, allora varrebbe:
CHA > (K/n )
e questo non si può avere perché K/nè
l'ampiezza dell'angolo (rettilineo) ottenuto dividendo K
in n angoli (rettilinei) uguali, ed è pertanto sempre
maggiore dell'angolo
curvilineo CHA, come risulta evidente
in Fig. 6.
Ma come abbiamo appena visto, Euclide risolve
elegantemente il problema della presenza di siffatti infinitesimi nel
quinto libro, tramite quel IV "termine" che dice che si parla di
rapporto fra due grandezze quando ognuna di esse supera l'altra se
sommata a se
stessa abbastanza volte. Rapportare angoli curvilinei e rettilinei
viene
quindi escluso, ed il problema evitato (l'idea dell'angolo curvilineo
come
"infinitesimo in atto " verrà comunque ripresa e studiata
più
tardi da vari autori, come, ad esempio,
Giordano Nemorario
, 1225-1260).
2° Problema: Gli infinitesimi e lo studio di aree e volumi.
Sembra che già fosse stato uso, in tempi precedenti (ad esempio in Democrito, vedi sez. 3) di approssimare figure curve con figure rettilinee dotate di un numero sempre maggiore di lati, finché essi non diventavano "infinitamente piccoli", ma un tale procedimento non poteva essere rigoroso se ricorreva all'uso di infinitesimi o infiniti.
Consideriamo per esempio il problema di
determinare l'area del cerchio; supponiamo di avere un cerchio di
raggio r e circonferenza C e si voglia dimostrare che
la sua area è ![]() .
.
Si può pensare di approssimare il cerchio
con poligoni regolari, vedi Fig. 5.a, suddivisi in triangoli uguali.
Notando che l'area del poligono è equivalente alla somma di
quella dei triangoli in Fig. 5.b, che è a sua volta equivalente
a quella dei triangoli in 5.c, da qui si ha che se il poligono ha
perimetro P ed a è
l'altezza dei triangoli, allora l'area del poligono è [ax
P/2] (che è l'area del triangolo in 5.c).
Fig. 5.a 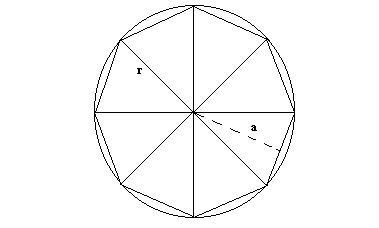
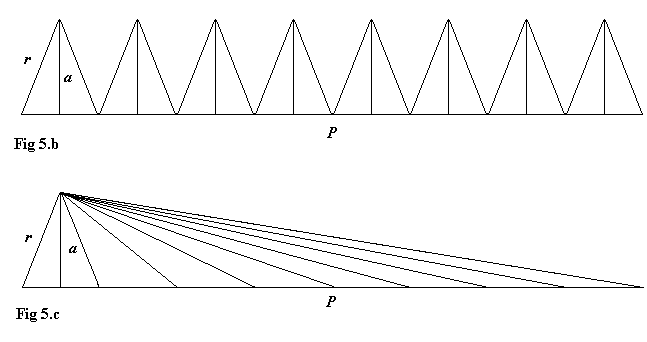
Se aumentiamo il numero dei lati del poligono la sua area e quella del cerchio saranno sempre più vicine, ed a si avvicinerà sempre di più ad r : pensando il cerchio come un "poligono con infiniti lati" (ognuno di lunghezza infinitesima), avremo che la formula trovata per l'area del poligono diviene quella che volevamo dimostrare per il cerchio (con P = C, a = r).
Ma naturalmente questa "dimostrazione" non ha nulla di rigoroso:
Che senso ha parlare di un poligono con infiniti lati?
Tali lati non avrebbero lunghezza nulla? Ed in
tal caso anche i corrispondenti triangoli non avrebbero area nulla?
Come aggirare queste difficoltà e dare un metodo per completare rigorosamente dimostrazioni del tipo di quella testé esposta?
Un modo fu dato da
Eudosso di Cnido (408?-355? a.C.), forse il maggior talento
matematico prodotto dall'Accademia
platonica.
L'idea di Eudosso consiste nel dimostrare il
risultato per assurdo
: cioè invece di dimostrare che l'area del cerchio
è ![]() , dimostrare che non può non essere
diversa da
, dimostrare che non può non essere
diversa da ![]() .
.
Il procedimento è questo: sia K
= ![]() ;
dobbiamo far vedere che è assurdo che l'area cercata sia
maggiore di K e che è parimenti assurdo che sia
minore di K. Avremo quindi che l'unica
possibilità rimasta sarà che l'area del cerchio sia
esattamente uguale ad K.
;
dobbiamo far vedere che è assurdo che l'area cercata sia
maggiore di K e che è parimenti assurdo che sia
minore di K. Avremo quindi che l'unica
possibilità rimasta sarà che l'area del cerchio sia
esattamente uguale ad K.
Per vedere che l'area del cerchio non è minore di K, basta che comunque si fissi una quantità X minore di K, l'area del cerchio risulti maggiore di X. Basterà quindi far vedere che per ogni quantità X minore di K possiamo trovare un poligono regolare inscritto nel cerchio (come in Fig. 5.a) la cui area sia maggiore di K . Poiché l'area del cerchio è ovviamente maggiore di quella del poligono, avremo che l'area del cerchio è anche maggiore di X .
Per la prova dettagliata (in linguaggio moderno) di quanto ora detto, cliccare QUI .
Questo metodo è detto metodo di Esaustione (questo termine non veniva usato dai Greci, ma venne introdotto nel XVII secolo) e permette di sfruttare l'idea che il cerchio è approssimabile con poligoni senza introdurre il concetto di infinito (sia evitando l'idea di "infiniti lati", che quella di "lati infinitesimi"); il prezzo di tale operazione è una certa lunghezza e complicazione nelle dimostrazioni (dovendo dimostrare una doppia negazione) che risultano però del tutto rigorose anche per gli standard odierni (il particolare esempio di applicazione del principio di esaustione dato sopra è posteriore ad Eudosso ed Euclide ed è dovuto ad Archimede).
Ritroviamo il metodo di esaustione descritto ed
impiegato ampliamente nel libro XII degli
Elementi di Euclide, ma il risultato su cui esso si basa appare nel
libro X, e si può enunciare così :
Se da una qualsiasi grandezza si sottrae una parte non inferiore alla sua metà, e dal resto si sottrae ancora non meno della sua metà, e se questo procedimento di sottrazione viene continuato, alla fine rimarrà una grandezza inferiore a qualsiasi grandezza precedentemente assegnata.
Questo risultato si ricava a sua volta da un postulato che non fu
esplicitamente espresso da Euclide come tale (ma dato come
proprietà definitoria dei rapporti fra grandezze, vedi sopra):
Date due grandezze diseguali e non nulle, la minore sommata a se stessa un numero sufficiente di volte, finirà per superare la maggiore.
Questa proprietà delle grandezze esclude che
possano esistere degli infinitesimi (perché in quanto tali
resterebbero minori di una grandezza finita anche se sommati a se
stessi un numero grande qualsivoglia di volte). La proprietà fu
enunciata esplicitamente
da Archimede (nel testo Quadratura della parabola, vedi
prossima
sezione) anche se egli la attribuisce ad Eudosso) ed è oggi
comunemente
nota come assioma di Archimede.
È con Archimede di Siracusa (287-212 a.C.) che la geometria del periodo ellenistico raggiunge le sue vette più alte, ed Archimende usa con abilità il metodo di esaustione riuscendo a calcolare aree e volumi. Ricordiamo, fra i tanti da lui dimostrati, il teorema che, secondo i suoi desideri, fu inciso sulla sua tomba:
Ogni cilindro la cui base sia il cerchio massimo di una sfera e la cui altezza sia uguale al diametro della sfera ha per volume i 3/2 del volume della sfera e per superficie totale i 3/2 di quella della sfera.Il metodo di esaustione sembrerebbe la riprova di ciò che aveva affermato Aristotele:
|
|
Con l'esaustione infatti i grandi geometri dell' antichità erano riusciti ad "aggirare l'infinito" secondo i dettami aristotelici e a non usarlo mai nelle dimostrazioni.
Archimede usa questo procedimento ad esempio per calcolare l'area del segmento di parabola (vedi Fig. 6), nel suo scritto Quadratura della parabola.
Abbiamo quindi visto che con l'Esaustione si
riuscì a calcolare aree di figure piuttosto complesse (gli
esempi che abbiamo visto sono fra i più semplici).
Eppure questo modo di procedere presenta un grosso limite:
|
|
L'esaustione è infatti un modo rigoroso per provare che una data quantità è l'area (o il volume, o il perimetro) cercato (come nell'esempio precedente per il cerchio), ma come determinare questa quantità? Ciò non viene in alcun modo suggerito dal metodo stesso. Nell'esempio del cerchio, il considerarlo come un poligono con infiniti lati non è rigoroso, ma dà l'idea che porta a determinarne l'area. Quindi l'esaustione è certamente rigorosa, ma non fertile: i risultati che permette di dimostrare devono essere intuiti per altre vie.
Fu proprio da Archimede (come nota L.L.Radice in [R ]), il più raffinato nell'uso del metodo di esaustione, che venne una descrizione della possibilità di un uso per quegli "infinitesimi" che Aristotele aveva bandito e che Archimede stesso non usò mai per le sue dimostrazioni. Infatti, nel 1906, venne ritrovata in una biblioteca di Istambul un'opera precedentemente sconosciuta del grande Siracusano: un breve trattato conosciuto oggi come Il metodo ove egli descrive un suo modo per "trovare teoremi" in geometria (non per dimostrarli!!), cioè una procedura euristica, non dimostrativa, di indagine geometrica (dal greco heuriskein, "trovare", "scoprire").
Nel trattato Archimede (oltre ad introdurre metodi "meccanici", che usano i baricentri delle figure ed il principio della leva, da lui scoperto) descrive come si può pensare ad esempio alle figure solide come composte dalle loro (infinite) sezioni piane, ognuna di spessore infinitesimo. Un primo esempio di questo metodo (che Archimede fa risalire a Democrito) è l'osservazione che piramidi diverse, ma di ugual base ed altezza, hanno lo stesso volume:
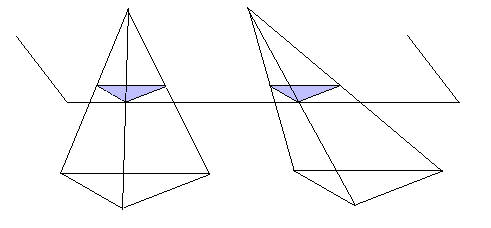
Notando che le piramidi hanno sezioni uguali se tagliate con piani paralleli alle basi, e pensando le piramidi come composte dalle loro infinite sezioni piane, si avrà che i due volumi devono essere uguali.
Archimede usa questo metodo per studiare molte figure (il segmento di parabola, ad esempio), ma è ben conscio che esso non ha nulla di rigoroso: egli scrive poi le dimostrazioni usando il solito metodo d'esaustione. Si ha quindi una specie di "doppio binario": da una parte gli infinitesimi per intuire le relazioni fra le figure e dall'altra l'esaustione per dimostrare rigorosamente ciò che si è scoperto. L'infinito attuale, eliminato dal "corretto ragionare", riappare come "metodo d'indagine". E riappare proprio come uno strumento quasi "naturale" nell' attività matematica, per quanto non rigoroso.
Archimede ha ben chiara la fertilità di questo suo modo di procedere, e su di esso scrive infatti (sempre ne Il metodo):
Sono convinto che porterà non piccola utilità nella matematica: confido infatti che alcuni dei matematici attuali o dei futuri, essendo stato loro mostrato questo metodo, ritroveranno anche altri teoremi da noi non escogitati.Purtroppo il libro di Archimede fu riscoperto solo recentemente, ed egli non usò altrove questo metodo, ma solo il principio di esaustione. Quindi i matematici medioevali e moderni non ne furono a conoscenza, ma è comunque possibile veder comparire saltuariamente l'uso di "infinitesimi" o "indivisibili" dal Medioevo fino al XVII secolo, quando il loro uso venne teorizzato ed essi largamente applicati (come vedremo nel capitolo seguente). Che questo uso fosse, come abbiamo già detto, in qualche senso "naturale" in matematica lo testimonia non solo il fatto che questa procedura sia stata "riscoperta" indipendentemente secoli più tardi, ma anche quanto scrive Evangelista Torricelli (uno appunto dei "riscopritori"), pur non potendo sapere quanto esattamente avesse intuito la realtà:
Che questa geometria degli indivisibili sia invenzione del tutto nuova, non oserei affermarlo. Crederei piuttosto che gli antichi geometri si siano serviti di questo modo nell'invenzione dei teoremi più difficili, benché nelle dimostrazioni abbiano seguito un'altra via, sia per occultare il segreto dell'arte, sia per non offrire agli invidi detrattori alcuna occasione per contraddirli .
(E.Torricelli, Opera Geometrica, 1644)
Una nota a parte merita un'opera minore di
Archimede, il Yammithz (in latino Arenarius),
ove egli introduce un originale sistema di numerazione per
rappresentare i grandi numeri, dandosi come obbiettivo quello di
dimostrare che il numero di granelli di sabbia nell'universo
è finito, e di dare una maggiorazione per tale numero. L'opera,
dedicata
al sovrano di Siracusa, Gelone, inizia così :
Alcuni pensano, o re Gelone, che il numero dei granelli di sabbia sia infinito per grandezza: parlo del numero dei granelli non solo della sabbia che é nei dintorni di Siracusa e nel resto della Sicilia, ma anche della sabbia sparsa su tutta la Terra... Ci sono altri, al contrario, che partono dall'affermazione sicura che questo numero non è infinito, ma che tuttavia non si potrebbe enunciarne un altro che sia più grande... Ebbene, io cercherò di provarti, attraverso delle dimostrazioni geometriche di cui potrai seguire i ragionamenti, che certi numeri che ho espresso... sorpassano non solo il numero di granelli di sabbia il cui volume è uguale a quello della Terra, ma anche il numero dei granelli di sabbia il cui volume è uguale a quello del cosmo.Il metodo di numerazione greca (come poi quello romano) non offriva metodi efficaci per esprimere e trattare numeri molto grandi; in questa opera Archimede elabora una sistemazione che gli permette di trattare numeri di enorme ordine di grandezza.
Il metodo si basa sulle miriadi di miriadi in base alle quali Archimede periodizza il sistema dei numeri (la miriade è pari a 104 = 10.000, e quindi una miriade di miriadi è pari a 108 , cioè cento milioni):
È da notare che in questo modo Archimede
introduce una regola con la quale si può andare avanti
indeterminatamente nello scrivere numeri sempre più grandi
(anche se egli non lo dice esplicitamente). Questo fatto risulta
elementare per il nostro metodo di rappresentazione, che ci abitua a
pensare il sistema dei numeri come un sistema "aperto", dove per
passare a numeri più grandi si tratta solo di aumentare il
numero delle cifre, ma ciò non é altrettanto semplice per
sistemi come quello
greco o romano, che devono introdurre sempre nuovi simboli per numeri
più grandi.
Dopo
aver descritto questo metodo di numerazione, Archimede dimostra un
teorema
sulle proporzioni (che grosso modo equivale alla uguaglianza 10n
.10m = 10n+m), e poi passa
al problema dei granelli di sabbia vero e proprio. Esso viene risolto
partendo dalla supposizione che il numero di granelli contenuto in una
sfera della grandezza di un seme di papavero sia minore di 10.000
(supposizione più che ragionevole), e poi utilizzando il fatto
che il rapporto fra i volumi di due sfere è uguale al rapporto
dei cubi dei loro raggi. In questo modo si trova una serie di
proporzioni fra volumi di sfere sempre più grandi, partendo dal
seme di papavero e arrivando alla sfera del cosmo
(cioè alla sfera avente per raggio la distanza Terra-Sole,
allora
valutata minore di 1010 stadi) ed a quella delle stelle
fisse
(qui Archimede utilizza l'ipotesi di Aristarco che il volume del cosmo
sia medio proporzionale fra quello della Terra e quello della sfera
delle
stelle fisse.)
Con questi calcoli, Archimede prova che il numero
dei granelli di sabbia contenuti
nel cosmo è minore di 1051, e quello contenuto nella
sfera delle stelle fisse è minore di 1063.
Abbiamo voluto dare questa breve descrizione
dell' Arenario perché esso illustra bene, in termini
matematici ed astronomici, le concezioni
Aristoteliche attorno all'infinito: l'impossibilità
dell'infinito
in atto (finitezza dell'universo) e la possibilità dell'infinito
potenziale (nel sistema dei numeri).
7. Dio e l'infinito in
atto: il medioevo cristiano.
Alla
decadenza della cultura greca seguirà una sostanziale
indifferenza
del mondo romano per la scienza pura. Dice Cicerone:
"I Greci ebbero il geometra nella più alta considerazione e nulla raggiunse fra loro progressi più brillanti della matematica. Noi invece abbiamo fissato come limite di questa arte la sua utilità per misurare e contare".
Si ha infatti nell'occidente europeo un lungo
periodo di stasi per la matematica, che proseguirà anche
nell'alto medioevo (il primo matematico europeo di rilievo sarà
il pisano
Leonardo Fibonacci (1170?-1250).
Una ripresa in grande stile degli interessi
matematici ed anche dei problemi riguardanti l'infinito non si
avrà fino all'età moderna,
di cui tratteremo nel prossimo capitolo. Quello a cui vogliamo
nondimeno
accennare qui sono le speculazione filosofiche su infinito ed
infinitesimi
da parte di scuole e personalità del medioevo cristiano. Tali
speculazioni giocheranno anche un ruolo non indifferente
nell'influenzare le vedute
dei matematici posteriori su questo tema, che resterà a lungo
"in
condominio" fra matematica e filosofia. Ciò si vedrà
specialmente
nell'età moderna, che annovera i medesimi nomi fra le più
eminenti personalità dei due campi.
Citiamo, primo fra tutti, S.Tommaso d'Aquino (1221-1274), il principale artefice della assimilazione della filosofia aristotelica nel pensiero cristiano. Come Aristotele, Tommaso respinge la possibilità di un infinito in atto in natura o in matematica: dove egli non osa seguire Aristotele è nel rifiuto di attribuire infinità anche a Dio.
Aristotele aveva sostenuto che il concetto di infinito è collegato con la categoria della quantità e quindi non poteva essere attribuito a Dio, il "Motore Immoto" della sua cosmologia. Tommaso invece afferma (nella sua Summa Theologica ), che Dio è infinito ed eterno ed incircoscrivibile , e specifica poi che si hanno due tipi di infinito: l'infinito "ex parte materiae" e quello "ex parte formae". L'infinito riconducibile alla idea di forma (non molto diverso dall'infinito in atto di Aristotele) è attribuibile a Dio, ed a lui solo. Invece tutte le cose create, proprio in quanto "fatte", hanno come caratteristica l'essere finite ed imperfette ed è quindi assurda anche l'idea di Dio che crea un oggetto infinito (quantitativamente o qualitativamente), in quanto "l'essere fatto, creato" è in contraddizione con l'essere infinito.
In questa linea di pensiero, come nella cosmologia precedente, anche l'universo è finito, senza che ciò contraddica l'onnipotenza di Dio, e quindi l'infinito "ex parte materiae" si può avere solo in senso potenziale, come in Aristotele.
Anche in matematica Tommaso esclude l'infinito in atto: in geometria con ragionamenti analoghi a quelli aristotelici ed in aritmetica praticamente negando il concetto di "insieme infinito".
Egli definisce un insieme (moltitudo) come una moltitudine di individui considerata come un unità, ed il numero come il risultato del contare gli elementi dell'insieme. Il concetto stesso di "numero infinito" risulta perciò contraddittorio (resterà considerato tale fino a Cantor, vedi cap. III).
L'escludere l'infinito dall'universo sensibile, negando a Dio la possibilità di creare qualcosa di infinito, non fu accettato supinamente all'interno della Chiesa: i francescani combatterono vigorosamente l'aristotelismo, e nel 1277 il vescovo di Parigi condannò numerose tesi averroiste, alcune delle quali proprie anche di Tommaso.
In particolare la ventinovesima delle tesi messe al bando dice che l'infinità di Dio è compatibile solo con la sua totale estraneità al divenire dell'universo, e che la sola manifestazione di tale infinità è quella della perfezione della forma.
In Inghilterra la condanna venne rinnovata dieci anni più tardi dall'arcivescovo di Canterbury, francescano come Riccardo da Middleton, che sostenne l'infinità potenziale dell'universo: egli affermò che Dio può produrre grandezze e dimensioni che crescano oltre ogni limite, purché in ogni istante la grandezza realizzata sia finita.
Solo nel 1325 i domenicani riuscirono ad ottenere
la revoca della condanna del 1277 e la canonizzazione di Tommaso. Col
passare del tempo le posizioni
dell'Aquinate diverranno sempre di più dottrina ufficiale, fino
a che egli verrà nominato (nel 1565) dottore della Chiesa.
Nel '300 ebbero grande rilievo in fisica e
matematica la scuola di Parigi e
quella di Oxford. A Parigi, Nicola Oresme (1323-1382) e Giovanni
Buridano
(1300-1360?) rividero in molte direzioni le teoria aristoteliche del
moto:
studiarono il cambiamento ed il tasso di cambiamento sia nei moti
(parlando
di moto uniforme intendendo "a velocità costante" e di
moto uniformemente difforme e cioè "ad accelerazione
costante"),
sia più in generale nei vari fenomeni fisici (calore,
temperatura).
La trattazione di Oresme è quantitativa ed usa la geometria, presentando in nuce un primo abbozzo di geometria analitica e di rappresentazione di grandezze tramite grafici.
Oresme studia anche le somme infinite, e nel suo Questiones
super Geometriam Euclidis considera la somma (detta serie
armonica):
|
|
dando una dimostrazione che essa non dà una somma finita. Il
procedimento è molto
semplice; Oresme confronta la (*) con la
|
|
Dove il termine 1/16 è ripetutto 8 volte,
e in genere il termine
2 -n è ripetuto (n-1)
volte.
Poiché ogni termine della (**) è minore o uguale del
rispettivo
termine della (*), si ha che se la somma della (**) è infinita,
così accadrà per la (*). Ma i termini della (**) si
possono raggruppare così :
|
|
ottenendo una somma in cui ogni addendo è pari ad 1/2, e
quindi una somma che, utilizzando un numero sufficiente di addendi,
è in grado di superare qualsiasi quantità prefissata,
quindi una somma il cui risultato non può essere finito.
È da notare che tale procedimento, per quanto sia
intuitivo e porti ad un risultato corretto, non è accompagnato
ad
alcuna teoria rigorosa di come operare con le serie (abbiamo visto
all'inizio
nella prima sezione esempi di come il riordinarle possa dare problemi).
Buridano è uno dei fondatori (o meglio, dei precursori) della moderna dinamica: si avvicina al concepire una specie di principio di inerzia con la sua teoria dell'impeto che egli sostituisce alla precedente idea aristotelica che sia l'aria a sostenere il moto di un oggetto che sia stato scagliato.
Buridano afferma che l'oggetto ha ricevuto un impeto (che sarebbe una "tendenza a muoversi") che poi viene smorzato dalla resistenza dell'aria o dalla gravità (se il proiettile è lanciato verso l'alto ). La grossa novità è che così si viene ad affermare che le forze intervengono a modificare i moti, invece di essere necessarie al loro proseguimento (ed in tal modo i moti non sono più incompatibili con l'esistenza del vuoto); inoltre Buridano applica la teoria dell' impeto anche alle sfere celesti, unificando moti terrestri e celesti sotto una stessa teoria. Egli afferma che Dio ha dato ai cieli un impeto iniziale ed essi si muovono da allora, senza bisogno della presenza delle "intelligenze celesti" (o angeliche) a mantenerne il moto.
In matematica, Buridano elabora un paradosso molto intrigante per discutere la presenza dell'infinito in atto negli enti geometrici: quello della linea gyrativa.
Si consideri un cilindro di altezza unitaria e lo si pensi suddiviso in una successione infinita di cilindri ottenuti tramite dimezzamenti successivi, e cioè cilindri di altezze 1/2, 1/4, 1/8, ...
Si disegni poi sul primo cilindro (di altezza 1/2) un'elica il cui passo sia 1/2 (vedi Fig. 8), si prolunghi l'elica su quello di altezza 1/4 con un elica di passo 1/4, e così via sugli altri cilindri.

La linea che si ottiene (che Buridano chiama appunto " linea gyrativa ") è composta di infiniti tratti di elica, ognuno dei quali ha lunghezza superiore a quella della circonferenza di base. La linea risulta quindi di lunghezza infinita; la questione è se si tratti di un'infinità potenziale (come quella della retta, sempre prolungabile ma mai pensabile nella sua interezza) od invece di un vero e proprio infinito in atto.
Se pensiamo il processo di suddivisione del cilindro come solo potenzialmente infinito (non c'è limite alle suddivisioni, ma ne consideriamo sempre un numero finito), siamo portati a considerare la linea come un infinito potenziale. D'altro canto se pensiamo al cilindro nella sua interezza possiamo concepire la linea come tracciata su di esso (oggi diremmo che la linea è un suo sottoinsieme) e perciò assegnata "tutta insieme" (per ogni punto del cilindro, siamo in grado di dire se esso appartiene o no alla linea); quindi la linea sarebbe un esempio di infinito in atto, effettivamente assegnato nella sua totalità.
Buridano riteneva di difficile soluzione il
problema di scegliere qui fra l'infinito in atto e quello potenziale e
non dette una risposta, ma è comunque significativo che il
considerare la presenza di un infinito assegnato effettivamente non
venga più considerata come un "tabù".
Nella scuola di Oxford segnaliamo Tommaso da
Bradwardine, che si occupò a fondo di matematica e
particolarmente del problema della continuità e degli
indivisibili. Le sue concezioni furono simili a quelle di Aristotele ed
egli polemizzò duramente con chi sosteneva dottrine atomistiche,
ritenendo che le grandezze continue sono composte da infiniti continui
dello stesso tipo, e non si possono ottenere componendo, integrando
degli
infinitesimi (forse Bradwardine è il primo ad usare il termine
"integrare"
in questo senso): Nullum continuum ex indivisibilibus infinitis
integrari
vel componi. Prima di lui posizioni simili erano state sostenute da
Ruggero Bacone e Duns Scoto.
Nonostante le posizioni aristoteliche e tomiste
siano prevalenti, l'idea della presenza dell'infinito in atto (o
dell'infinitesimo) nella matematica e nel mondo sensibile non scompare
mai. Un paradosso simile a quello di Buridano è escogitato da
Gregorio da Rimini (1300?-1358) per riaffermare la possibilità
che Dio crei un infinito attuale: suddividiamo un'ora in intervalli di
1/2, 1/4, 1/8 ... di ora (come abbiamo
fatto per il cilindro) e supponiamo che nel primo intervallo Dio crei
una pietra, nel
secondo ne raddoppi il volume, nel terzo raddoppi il volume ottenuto e
via
così . Cosa otterremo alla fine dell'ora? Una pietra
infinitamente
grande!
E supporre che Dio non possa raddoppiare il volume della pietra in un intervallo di tempo piccolo quanto si vuole sarebbe limitarne l'onnipotenza. Quindi l'onnipotenza di Dio implica la possibilità, da parte sua, di creare degli infiniti in atto.
Gregorio era un agostiniano, ed è proprio
in S.Agostino (354-430 d.C.) che troviamo una delle prime affermazioni
dell'attuabilità di infiniti effettivi, perlomeno in mente
Dei. Troviamo infatti nel suo De
Civitate Dei :
I numeri sono disuguali tra loro e diversi, e presi singolarmente sono finiti, e tutti quanti [insieme] sono infiniti. Dio, allora, a causa della [sua] infinità conosce tutti i numeri: e che forse la scienza di Dio perviene solo ad una certa somma di numeri, et ignora gli altri? Chi sosterrebbe ciò, anche se del tutto demente ?
8. Il trionfo
dell'infinito in atto nell'età moderna.
Un uso pieno e senza restrizioni dell'infinito
attuale si trova poi in Nicola Cusano (1401-1464), che seppe riprendere
i motivi del neoplatonismo inserendoli nella nuova cultura umanistica
rinascimentale.
Il Cusano parla tranquillamente del cerchio come di un poligono con infiniti lati, ed usa argomenti di questo genere nelle sue speculazioni matematiche, le quali vengono a mancare del rigore tipico delle costruzioni della geometria greca ed anche della filosofia scolastica. Anche se Nicola Cusano non dette apprezzabili contributi diretti alla matematica è comunque per la via da lui praticata, con l'uso sempre più esteso dei concetti di infinito e soprattutto di infinitesimo, che nascerà il calcolo infinitesimale (che dovrà poi attendere fino al secolo scorso per una sua sistemazione veramente rigorosa, come vedremo nel prossimo capitolo).
Cusano parla di Dio come dell'infinito in cui gli opposti vengono a coincidere e del mondo come dell' "esplicazione" (explicatio) di Dio nella molteplicità e di una "imitazione" della divinità. Seguendo tale idea il mondo non può che essere infinito e privo di centro e quindi si ha il rifiuto completo della cosmologia aristotelica e tomista.
Un tipico esempio del Cusano di come l'infinito, l'Assoluto, sia misura di tutto è dato dal considerare la retta come un cerchio di raggio infinito (vedi Fig. 9):
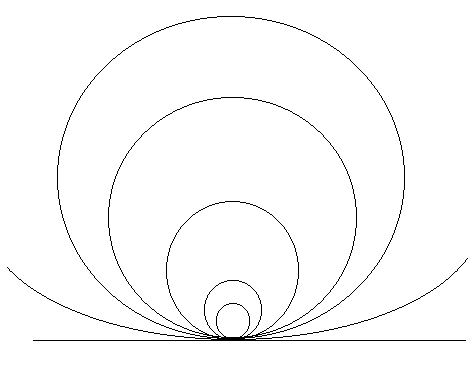
Nel retto scompare ogni "curvità", ma la misura dell' "essere curvo" è data proprio dall' aderenza alla retta. L'essere più o meno curvo, l'essere misurabile, è dato solo per il finito (la finita curvatura dei cerchi) e non si dà per l'infinito (la retta), che resta però termine di misura di questa proprietà.
Nel Cusano (uomo del Rinascimento) si ha più apertamente ciò che in vari pensatori medioevali (specialmente neoplatonici) era già apparso, e cioè:
guardare all'infinito non come a qualcosa di indeterminato, caotico e privo di ordine e perfezione (come nell'apeiron aristotelico) ma come ad un Assoluto.Una concezione simile si trovava già in Melisso che costituisce, insieme a Zenone, il principale continuatore della scuola parmenidea.
L'infinito diviene quindi una totalità a cui tendere con il nostro intelletto in un processo conoscitivo asintotico , cioè in un graduale avvicinamento infinito che non può mai essere un raggiungimento pieno a causa della finitezza della nostra mente.
Il punto di vista del Cusano verrà poi
ripreso ed ampliato da Giordano Bruno (1548-1600) che sosterrà,
ancora più arditamente, la teoria dell'infinità
dell'universo e del numero dei mondi, fin quasi ad approdare ad una
"religione dell'infinito" (Geymonat), come è
mostrato in questo inizio del quinto dialogo del suo De la Causa,
Principio
e Uno , che è quasi un inno all'Universo infinito (non
all'infinità di Dio):
È dunque l'universo uno, infinito, inmobile. Una è la possibilità assoluta, uno l'atto,... uno lo ente, uno il massimo ed ottimo. Non può sminuire o crescere, atteso che è infinito; a cui come non si può aggiongere, cossì è da cui non si può suttrarre, per ciò che l'infinito non ha parte proporzionabili...Perché se vuoi dir parte de l'infinito, bisogna dirla infinita; se è infinito, concorre in uno essere con il tutto: dunque l'universo è uno, infinito, impartibile.
Nonostante l'affinità con le posizioni del
Cusano, che era anche cardinale, Bruno vive in un periodo di molta
minor
tolleranza, e le sue posizioni (non solo quelle sull'infinito,
naturalmente)
lo porteranno sul rogo.
A testimoniare come il '600 sia veramente un
secolo che costituisce un
punto di svolta per gran parte del pensiero occidentale, notiamo come
esso
si apra con il rogo di Bruno (Febbraio 1600), e le condanne al sistema
copernicano, mentre alla sua fine l'idea che il mondo sia infinito
è ormai penetrata sia nella fisica di Cartesio che in quella di
Newton: l'Universo di Newton è ormai uno spazio infinito (senza
"centro", né nella Terra né nel Sole), regolato da leggi
matematiche (la geometria euclidea ed il principio di gravitazione
universale). In campo più strettamente matematico sin dalla fine
del secolo l'uso di procedimenti infinitesimali sarà ormai
giunto ad essere sistematizzato e diverrà uno
dei principali campi della ricerca in matematica.
[DAA] G.Arrigo, B.D'Amore: Infiniti. Franco Angeli, Milano, 1992.
[Be] E.T.Bell: I grandi matematici. Sansoni, Firenze, 1966.
[ BFTR] U.Bottazzini, P.Freguglia, L.Toti Rigatelli: Fonti per la storia della matematica. Sansoni, Firenze, 1992.
[R] L.L.Radice: L'Infinito. Editori Riuniti, Roma, 1981.
[Z] P.Zellini: Breve storia dell'infinito. Adelphi, Milano, 1980.