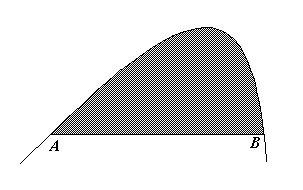
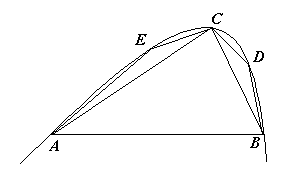
Archimede  usa il procedimento di esaustione per calcolare l'area del segmento di parabola, nel  suo scritto Quadratura della parabola : (naturalmente la dimostrazione  che diamo qui non segue letteralmente quella di Archimede, ma la traduce in linguaggio e simbologia attuale).
                          Fig. 6                                                                      Fig. 6.a
 

    Si vuole determinare l'area del segmento di parabola delimitato dal segmento AB  (vedi Fig. 6). A tal scopo si traccia il triangolo  ABC  inscritto alla parabola (cioè il triangolo formato prendendo il punto C come il punto sull'arco di parabola che è  più distante dal segmento AB ), e su di esso ancora dei triangoli ( AEC  e  CDB costruiti in modo analogo) inscritti alla parabola (Fig. 6.a).

    La dimostrazione si avvale di vari lemmi (dei quali non ripercorreremo la dimostrazione):

Lemma 1:  L'area del triangolo inscritto è maggiore di metà dell'area del segmento di parabola (cioè, nell'esempio in figura, l'area del triangolo ABC è maggiore di metà dell'area tratteggiata in Fig. 6).

Lemma 2:  La somma delle aree dei triangoli AEC  e  CDB è uguale  ad un quarto dell'area di  ABC.

    I due lemmi si dimostrano utilizzando le proprietà geometriche della parabola.

Sia ora  S l'area cercata (quella di Fig. 6); A 0 l'area del triangolo ABC , A 1 l'area coperta dai triangoli AEC  e  CDB , A2 l'area che si copre ripetendo la costruzione su tutti i lati  AE , EC, CD, DB e così via per  A 3 , A4 , ... , A n .   Ad ogni passo il numero dei triangoli raddoppia, ma la somma di essi è un quarto di quelli del passo precedente, cosicché abbiamo:

Lemma 3:  Sia  A0,A1 ,A2, ... ,A n , una successione di grandezze, ognuna quadrupla della successiva.  allora:

Esercizio 4:  Dimostrare il Lemma 3 (Suggerimento: Usare il principio di induzione).

Teorema :  S =  .

Dimostrazione:  Ovviamente la dimostrazione odierna consisterebbe nel far vedere che la serie   A0+A 1+ A2+ ... + An+ ...  converge a  .  Ma noi seguiremo la dimostrazione di Archimede, usando il metodo di esaustione.
    Sia, per assurdo,  S >  , inoltre poniamo  E = S -     ed    En = S - ( A 0+A1+ A2+ ... + A n );   avremo allora, per ogni n>0: S =  + E = A0+A1+ A2 + ... + An+ En  .
    Per il Lemma 1, ad ogni passo l'area  E n si riduce di più della metà quindi (per il postulato di Archimede), per n abbastanza grande si può arrivare ad avere  E n < E , e ciò implica (dall'uguaglianza sopra) che  < A0+A 1 + A2+ ... + An, il che è assurdo per il Lemma 3.

    In modo analogo si può dimostrare che è assurdo supporre   S <  , e quindi il teorema è dimostrato.

Esercizio 5:  Dimostrare anche l'assurdità di   S <  .