Finora si è visto come verificare se una successione ha limite o meno applicando direttamente la definizione e le sue conseguenze. Con tali metodi, però, non è possibile affrontare lo studio delle successioni che non sono estremamente semplici: i calcoli diventerebbero, infatti, troppo laboriosi e in certi casi si dovrebbe quasi indovinare l’andamento della successione.

Si vedranno ora dei metodi (attraverso otto teoremi fondamentali) che permettono di semplificare notevolmente il calcolo dei limiti e che analizzano il comportamento delle successioni attraverso le quattro operazioni elementari e la relazione di disuguaglianza.

I primi due teoremi mostrano un concetto che appare sufficientemente intuitivo: la somma dei limiti è uguale al limite della somma, il prodotto dei limiti è uguale al limite del prodotto dei limiti e allo stesso modo (quando possibile) si può fare per il quoziente.

 ________________________________________________________________________

TEOREMA (4.1)  Siano  (a_n) e  (b_n) due successioni di numeri reali tali che

   ,    .

Allora si hanno le seguenti proprietà:

1)   

2)    

3)     , se  e   .

 ________________________________________________________________________

Dimostrazione

1)      Si osserva che, poiché:

 : ,

 : ,

allora:

 : ,

2)      Allo stesso modo, con le condizioni di 1), si ottiene:

 :

,

In definitiva (per l’arbitrarietà di ε) si è provato ciò che si voleva, essendo:

 : ,

3)      E’ sufficiente, in questo caso, provare che  se  e  . Infatti, se ciò è vero, allora, per il punto precedente:

.

Si osserva prima di tutto che, al solito:

 : ,

Allora, fissato ε, per :

Scelto :

Ora, dunque,  : ,

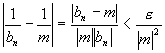e ciò prova quanto si voleva.

_________________________________________________________________________

TEOREMA (4.2)  Siano  (a_n) e  (b_n) due successioni di numeri reali.

1)     a)  Se  e , allora .

b)     Se  e , allora .

2)   a)  Se  e , allora .

b)     Se  e , allora .

c)      Se  e , allora .

d)     Se  e , allora .

3)  a)  Se  e , allora .

b)     Se  e , allora .

4)  a)  Se  e  con , allora .

b)     Se  e  con , allora .

5)  a)  Se  e   , allora .

b)     Se  e  , allora .

6)  a)  Se  e  , allora .

b)     Se  e  , allora .

_________________________________________________________________________

Omettiamo la dimostrazione per questo teorema in quanto molto tecnica e lunga (anche se il teorema stesso è molto utile nel calcolo dei limiti). 

Si può osservare che alcuni coppie di successioni non vengono menzionati: ad esempio, se  e , allora non è possibile ricavare alcun asserto generale sulla successione . Approfondiremo adeguatamente questo tema nell’ultimo paragrafo, in quanto ciò rientra in quelle che diremo forme indeterminate (vedi il paragrafo Risoluzioni di forme indeterminate).

ESEMPI (4.1)

Ora vedremo alcuni teoremi che ci mostrano alcune disuguaglianze notevoli sui limiti di successioni.

_________________________________________________________________________

TEOREMA (4.3) (della permanenza del segno)

Sia  (a_n)  una successione di numeri reali convergente al limite  l.

1)     Se , esiste   tale che:

,

2)     Se , esiste  tale che:

,

_________________________________________________________________________

Dimostrazione

Per la definizione di limite:

, : ,

Scelto si ha:

,

Se , , .

Se , , .

_________________________________________________________________________

TEOREMA (4.4)  Siano  (a_n) e  (b_n) due successioni di numeri reali tali che

  ,  . 

1)     Se , allora esiste , tale che , .

2)     Se  ,  allora si ha che .

_________________________________________________________________________

Dimostrazione

1)      Per i due teoremi precedenti 4.1 e 4.3, si osserva che  e allora esiste   tale che ,   e cioè , .

2)      Se si avesse , allora esisterebbe   tale che ,  e ciò sarebbe un assurdo in quanto incompatibile con l’ipotesi.

 _________________________________________________________________________

TEOREMA (4.5) (dei “carabinieri”)

Siano  (a_n) ,  (b_n) e (c_n)  successioni di numeri reali tali che:      ,

Se si ha che:

allora anche:

_________________________________________________________________________

Dimostrazione

Per la definizione di limite:

, : ,

, : ,

Quindi:

, : ,

Ciò prova così che .

_________________________________________________________________________

Ad esempio, la successione  tende a 0 in quanto “compresa” tra le due successioni  e , che convergono entrambe a 0, come è evidenziato dalla figura seguente.

 _________________________________________________________________________

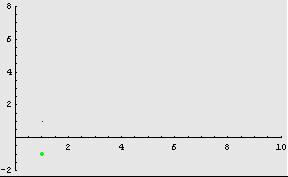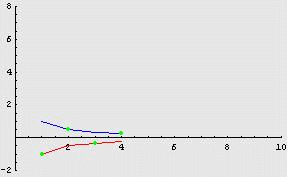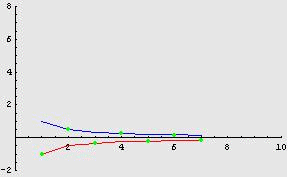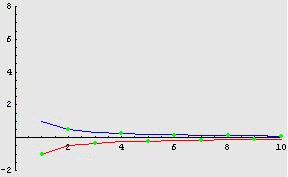
TEOREMA (4.6)  Siano  (a_n) e  (b_n) due successioni di numeri reali.

1)     Se  e , , allora .

2)     Se  e , , allora .

_________________________________________________________________________

Dimostrazione

1)      Per la definizione di limite:

, : ,

Allora si ha che:

, : ,

e così . 

2)      Allo stesso modo, sempre per la definizione di limite:

, : ,

e dunque:

, : ,

Allora .

 _________________________________________________________________________

ESEMPI (4.2)

Diamo, infine, alcuni cenni sul concetto di successione limitata (non addentrandoci in questioni più complicate che non hanno comunque lo scopo di risolvere direttamente il calcolo dei limiti, che è in sostanza ciò che ci interessa).

 _________________________________________________________________________

DEFINIZIONE (4.7)

1)     Una successione reale  si dice limitata superiormente se esiste  tale che  .

In tal caso, si dice estremo superiore di  il numero reale:     

2)     Una successione reale  si dice limitata inferiormente se esiste  tale che  .

In tal caso, si dice estremo inferiore di  il numero reale:    

3)     Una successione reale si dice limitata se è sia superiormente limitata sia inferiormente limitata.

4)     Se una successione reale  non è limitata superiormente, si pone:    

5)     Se una successione reale  non è limitata inferiormente, si pone:   

Osserviamo che, dalla definizione di limite, segue che:

-         se , allora

-         se , allora

 _________________________________________________________________________

TEOREMA (4.8)  Una successione reale convergente è limitata.

_________________________________________________________________________

Dimostrazione

Sia  una successione convergente al limite . Allora, per definizione:

, :  ,

Scelto :

:  ,

Dunque, si ottiene che:

,

Posto  e , si ha proprio:

, ,

da cui si conclude che la successione è limitata.

 _________________________________________________________________________

Naturalmente una successione limitata può non essere convergente: ad esempio, abbiamo visto che  è oscillante, pur essendo, però, limitata.