Si può osservare che alcune
successioni reali hanno la particolare proprietà di tendere ad
un valore ben
preciso, cioè, quanto più aumenta l’indice n di una successione 
,
tanto più essa sembra avvicinarsi ad un numero reale ben
preciso.
Consideriamo, ad esempio, la
successione 
;
all’aumentare del valore di
n, il valore di 
tende
a 0. Infatti, è costituita dalla successione di
numeri positivi:
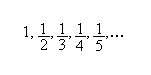
i quali sono sempre più vicini al valore 0, come evidenziato dalla seguente animazione:
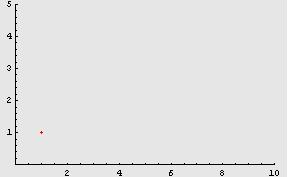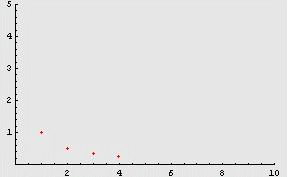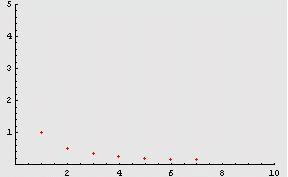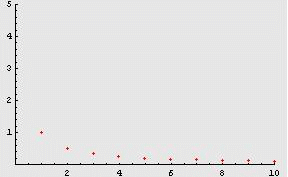
Appare naturale,
dunque,
introdurre il concetto di limite
di una successione: un numero reale l
a
cui la
successione tende all’aumentare
di n (un
valore, però, non necessariamente mai “raggiunto” da
un
termine =
l).
DEFINIZIONE
(2.1)
Sia 
una
successione di
numeri reali. Si dice che tende
al limite 
o che
converge a tale
limite se è tale che:
,
:
,
.
In tal caso, si
dice che è
una successione
convergente (o
ammette
limite finito) e si scrive:
.
Come si può
vedere negli
esempi seguenti, la definizione di convergenza di una successione
è più
complicata delle osservazioni intuitive, ma, nonostante l’aspetto
più formale,
è del tutto equivalente.
Come già
mostrato per le
successioni convergenti, anche altre successioni hanno un
“andamento”
altrettanto regolare; tuttavia, i termini di tali successioni,
anziché
avvicinarsi indefinitamente ad un valore limite, tendono ad assumere
valori
sempre più elevati all’aumentare dell’indice.
Consideriamo ad esempio la
successione 
.
1, 2, 3, 4, 5, ...
che procede
“all’infinito”.
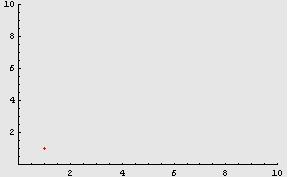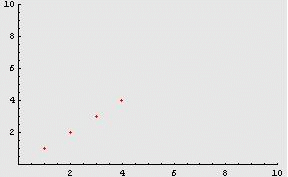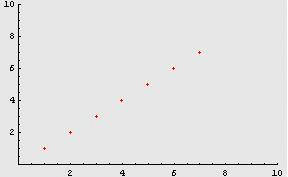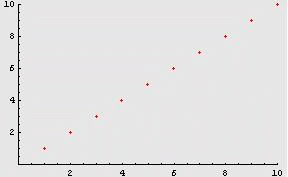
La stessa
osservazione può
essere applicata a successioni i
cui termini tendono
ad assumere valori negativi in valore assoluto sempre più
elevati al crescere
di n.
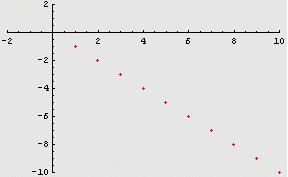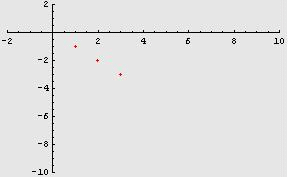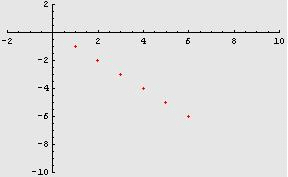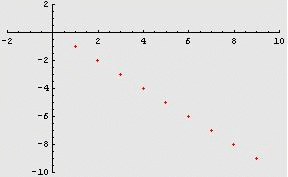
Ad esempio,
osserviamo la
successione “opposta” della precedente 
. “si
allontana” dallo
0. Si genera, infatti, la successione di interi negativi:
Possiamo,
così, introdurre il
concetto di divergenza di una successione reale.
DEFINIZIONE
(2.2) Sia una
successione di
numeri reali.
1) Si
dice che tende
a 
o
che diverge
positivamente se è tale che:
,
:
,
In
tal caso, si dice che è
una successione
divergente positivamente
(o
ammette limite )
e si scrive:
.
2) Si
dice che tende
a 
o che
diverge
positivamente se è tale che:
,
:
,
In
tal caso, si dice che è
una successione
divergente negativamente
(o
ammette limite )
e si scrive:
.
Anche nel caso
delle
successioni divergenti, gli esempi aiutano a chiarificare come la
definizione
formale è equivalente ai concetti intuitivi.
Il fatto che una
successione
possa essere convergente o divergente non implica affatto che per ogni
successione debba ammettere limite. Esistono, cioè, molte
successioni che non
hanno limite.
DEFINIZIONE
(2.3) Una successione che non è convergente
e non è né
divergente positivamente né negativamente si dice che è
una successione che non
ha limite o che è una successione
oscillante.
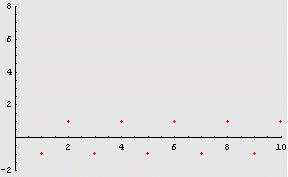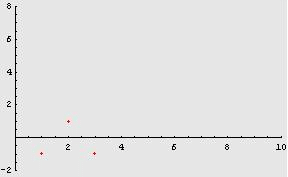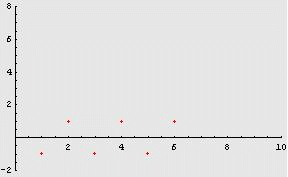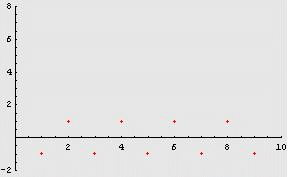
Consideriamo, ad
esempio, la
successione 
.
Essa assume
alternativamente
i valori 1 e -1, indefinitamente. Non appare "ragionevole" che tale
successione
abbia limite: non si avvicina a nessun valore.
Dimostrare
formalmente che
una successione è oscillante con gli strumenti che abbiamo
finora è piuttosto
complicato, come mostrato negli esempi.
Nei capitoli
successivi
vengono mostrate alcune nozioni che permettono di provare che una
successione
non ha limite in maniera più veloce ed elegante.
