Esempi di successioni oscillanti

1)         

    Supponiamo per assurdo che la successione converga ad un limite l. Allora, fissato un , applicando la definizione di convergenza, per n = 2k , si avrebbe | 1- l | < e  , mentre per n = 2k+1 ,  si avrebbe | -1- l | < e , ossia | 1+ l | < e .

Sviluppando le disuguaglianze, si otterrebbe:

1 - e < l < 1 + e

-1 - e < l < -1 + e

    Tali disuguaglianze, però varrebbero per ogni e > 0 e ciò sarebbe assurdo perché si dovrebbe avere simultaneamente: 

l = 1   e  l = -1.

    E’ evidente che la successione non può divergere, dal momento che essa assume solamente i valori 1 e -1: scegliendo M > 1, la definizione di divergenza a non può essere applicata, così come la definizione di divergenza a .

2)        a_n = sen(n)

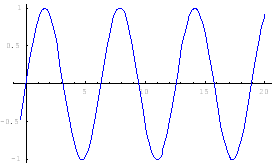
    Supponiamo per assurdo che la successione converga al valore l. Fissato _,   equivarrebbe a . E’ chiaro che sarebbe impossibile che ciò si verificasse per ogni n più grande di un certo n(ε), poiché la funzione sen x assume tutti i valori tra 1 e -1 con una periodicità pari a 2π. Quindi, ad esempio, scelto , non esiste alcun n(ε) per cui , .

    La successione non può nemmeno essere divergente, poiché (basta scegliere, ad esempio, M > 1) .

Con un analogo procedimento si può vedere che la successione  è oscillante.