Sezione: Discussione alla Weierstrass
D'ora in avanti assumeremo che la risultante delle forze 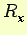 sia una funzione di classe
sia una funzione di classe
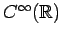 .
.
Ricaviamo
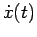 dalla legge di conservazione dell'energia:
dove il segno della radice è determinato come vedremo dalle condizioni iniziali.
dalla legge di conservazione dell'energia:
dove il segno della radice è determinato come vedremo dalle condizioni iniziali.
Assegnate le condizioni iniziali
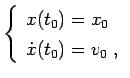 |
(3.1) |
possiamo innanzitutto distinguere due casi:
-
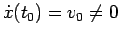
-
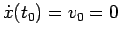
Caso 1
Il segno della velocità iniziale
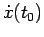 determina il fatto che all'istante
determina il fatto che all'istante 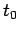 il moto sia diretto (nel verso positivo dell'asse
il moto sia diretto (nel verso positivo dell'asse 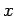 ) o retrogrado (nel verso negativo di
) o retrogrado (nel verso negativo di 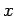 ). Possiamo dunque orientare l'asse
). Possiamo dunque orientare l'asse 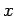 in modo che sia
in modo che sia
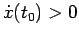 .
.
Per continuità esiste
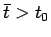 tale che
tale che
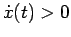 ,
,
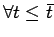 .
.
Allora
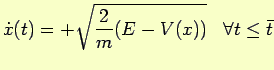 .
.
Poniamo ora
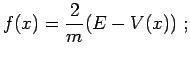 quindi
quindi
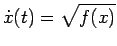 |
(3.2) |
e
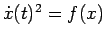 .
.
Osservazione 3.1
Poichè 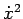 non può essere negativa, gli intervalli di
non può essere negativa, gli intervalli di 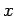 in cui il moto è consentito sono quelli per cui si ha
in cui il moto è consentito sono quelli per cui si ha
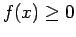 , ossia
, ossia
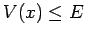 .
.
Tali intervalli potranno essere visualizzati tracciando il grafico della funzione 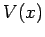 nel piano
nel piano 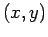 e la retta orizzontale
e la retta orizzontale 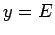 : le regioni ammissibili di
: le regioni ammissibili di 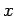 saranno quelle dove il grafico di
saranno quelle dove il grafico di 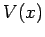 sta al di sotto della retta
sta al di sotto della retta 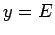 e tali tratti saranno finiti o infiniti a seconda che il corrispondente intervallo di
e tali tratti saranno finiti o infiniti a seconda che il corrispondente intervallo di 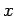 sia finito oppure no.
sia finito oppure no.
Esempio 3.1
Dato un potenziale come in fig.
3.1 notiamo che le regioni ammissibili sono solo quelle evidenziate in rosso.
Figura 3.1:
Regioni ammissibili di x
|
|
Osservazione 3.2
Per lo stesso motivo l'energia totale
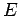
può assumere solo i valori che soddisfano la condizione
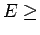 inf
inf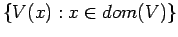
Esempio 3.2
Dato un altro potenziale come in fig.
3.2 che ammette un minimo assoluto
m notiamo che i valori ammissibili per
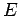
devono soddisfare la condizione
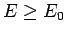 = m
= m.
Figura 3.2:
Valori ammissibili
|
|
Dato
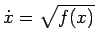 distinguiamo ora i casi:
distinguiamo ora i casi:
- 1.1
-
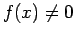
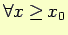
- 1.2
-
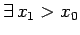 t.c.
t.c. 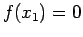
Caso 1.1
In questo caso si ha 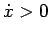
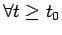 , cioè il punto materiale ha velocità positiva quindi il moto è diretto
, cioè il punto materiale ha velocità positiva quindi il moto è diretto
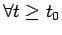 , cioè il punto si muove sempre nella direzione positiva dell'asse
, cioè il punto si muove sempre nella direzione positiva dell'asse 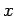 .
.
Figura 3.3:
Moto unidimensionale lungo x
|
|
Sia ora 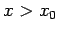 un punto arbitrariamente fissato sulla retta.
un punto arbitrariamente fissato sulla retta.
Calcoliamo il tempo 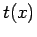 impiegato da
impiegato da 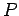 a raggiungere la posizione
a raggiungere la posizione 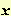 .
.
Dalla 3.2 si ha:
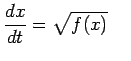
cioè
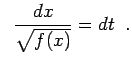
Integrando da 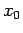 a
a 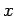 otteniamo:
Assumendo per semplicità
otteniamo:
Assumendo per semplicità 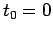 troviamo
troviamo
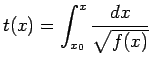 |
(3.3) |
L'integrale al membro di destra di 3.3 è finito, in quanto la funzione integrande è continua su
![$ [x_0,+\infty]$](img296.png) e quindi limitata su
e quindi limitata su ![$ [x_0,t]$](img297.png) ,
,
 .
.
Questo ci permette di concludere che il punto  impiega un tempo finito a raggiungere una qualunque posizione sull'asse
impiega un tempo finito a raggiungere una qualunque posizione sull'asse 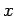 a destra della configurazione iniziale. Quindi il moto di
a destra della configurazione iniziale. Quindi il moto di 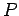 si svolge secondo questa modalità: parte da
si svolge secondo questa modalità: parte da 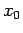 con velocità positiva e percorre tutto l'asse
con velocità positiva e percorre tutto l'asse 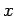 di moto diretto senza mai fermarsi, raggiungendo prima o poi, in un tempo più o meno lungo (ma finito!) una qualunque postazione preassegnata.
di moto diretto senza mai fermarsi, raggiungendo prima o poi, in un tempo più o meno lungo (ma finito!) una qualunque postazione preassegnata.
Tale moto è detto aperiodico e, nel caso specifico, diretto.
Caso 1.2
Sia
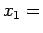 min
min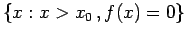 il più piccolo valore di
il più piccolo valore di 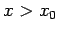 in cui la
in cui la 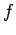 (e quindi la velocità) sia nulla.
(e quindi la velocità) sia nulla.
Figura 3.4:
Moto unidimensionale lungo x
|
|
Per quanto visto nel caso 1.1 possiamo subito affermare che il punto materiale raggiunge tutte le posizioni precedenti a 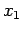 in un tempo finito più o meno lungo; si ha infatti di nuovo
in un tempo finito più o meno lungo; si ha infatti di nuovo
Essendo 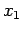 il "`primo"' valore di
il "`primo"' valore di 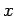 in cui
in cui 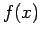 si annulla si avrà invece che il tempo
si annulla si avrà invece che il tempo
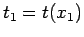 impiegato a raggiungere
impiegato a raggiungere 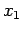 è dato da un integrale generalizzato:
è dato da un integrale generalizzato:
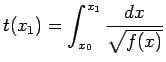 |
(3.4) |
La convergenza di questo integrale dipende dalla molteplicità di 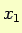 come radice di
come radice di 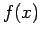 .
.
Si distinguono perciò due ulteriori sottocasi:
- 1.2.1
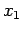 è una radice multipla di
è una radice multipla di 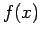 ;
;
- 1.2.2
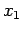 è una radice semplice di
è una radice semplice di 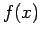 .
.
Caso 1.2.1
Sia dunque 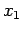 radice dell' equazione
radice dell' equazione 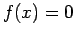 di molteplicità
di molteplicità 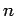 , ovviamente
, ovviamente 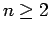 ,
, 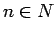 . Poichè
. Poichè
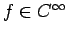 per ipotesi possiamo allora scrivere
per ipotesi possiamo allora scrivere 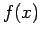 nella seguente forma:
nella seguente forma:
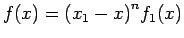 |
(3.5) |
con 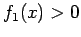 ,
,
![$ \forall\in [x_0,x_1]$](img314.png) .
Ricordando la 3.2 e la 3.5 si può scrivere
Dalla 3.4 si ha allora
.
Ricordando la 3.2 e la 3.5 si può scrivere
Dalla 3.4 si ha allora
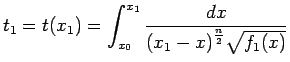 |
(3.6) |
L'integrale generalizzato 3.6 è divergente perchè la funzione integranda
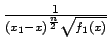 è un infinito di ordine
è un infinito di ordine
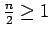 rispetto all'infinito campione
rispetto all'infinito campione
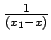 per
per
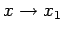 .
.
Dunque
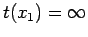 , cioè il punto materiale impiega un tempo infinito a raggiungere la posizione di ascissa
, cioè il punto materiale impiega un tempo infinito a raggiungere la posizione di ascissa 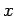 . In altre parole
. In altre parole 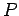 non raggiunge di fatto
non raggiunge di fatto 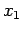 , se non asintoticamente, cioè al limite per
, se non asintoticamente, cioè al limite per
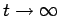 .
.
Concludiamo che nel caso di radice multipla si ha un moto asintotico verso il punto di ascissa 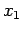 , a cui il punto si avvicina sempre più senza mai raggiungerlo.
, a cui il punto si avvicina sempre più senza mai raggiungerlo.
Osservazione 3.3
Dalla
3.5 segue che se
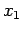
è una radice di
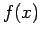
essa è multipla se e solo se
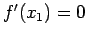
, o equivalentemente
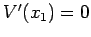
. Pertanto dal Teorema
3.1 si ha che una radice di
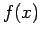
è multipla se e solo se è una configurazione di equilibrio.
Caso 1.2.2
Sia ora 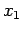 radice semplice dell'equazione
radice semplice dell'equazione 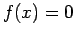 , ciò significa che
, ciò significa che
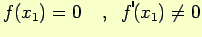 |
(3.7) |
per cui 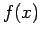 , per
, per
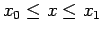 , può essere scritta come
, può essere scritta come
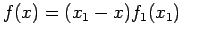 |
(3.8) |
con 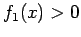 ,
,
![$ \forall x\in[x_0,x_1]$](img328.png) .
.
Procedendo come prima, si ha
per cui, separando le variabili, ed integrando ambo i membri si ottiene
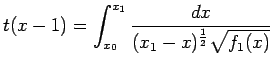 |
(3.9) |
Anche questo è un integrale generalizzato, ma ora l' infinito è di ordine
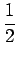 , per cui l'integrale converge.
, per cui l'integrale converge.
Dunque il punto impiega un tempo finito per raggiungere la posizione 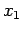 e all'istante
e all'istante 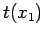 si ferma,
si ferma, 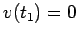 .
.
Ci chiediamo così come si comporterà il punto materiale dopo l'istante di arresto 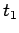 .
.
Per saperlo occorre studiare il segno di
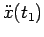 .
.
Osserviamo che
Ossia l'accelerazione è esprimibile in funzione di 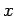 :
:
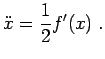 |
(3.10) |
Figura 3.5:
Accelerazione
|
|
Allora dalla 3.8 si ha
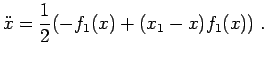 |
(3.11) |
Calcolando la 3.11 per 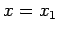 si ottiene, ricordando anche la 3.7,
si ottiene, ricordando anche la 3.7,
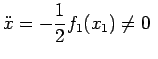
e in particolare
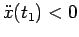
in quanto
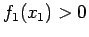 .
.
Ne segue che
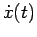 è decrescente in un intorno di
è decrescente in un intorno di 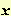 , ed essendo
, ed essendo
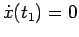 si avrà che esiste
si avrà che esiste 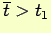 tale che
tale che
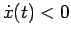
![$ \forall t\in]t_1,\bar{t}[$](img345.png) .
.
In generale possiamo affermare che quando il punto materiale incontra una radice semplice, ed ha un istante di arresto, inverte la direzione del moto essendo l'accelerazione 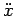 diversa da zero. A questo punto lo studio del moto riprende ripetendo l'analisi già fatta e si arriva facilmente alle conclusioni che seguono
diversa da zero. A questo punto lo studio del moto riprende ripetendo l'analisi già fatta e si arriva facilmente alle conclusioni che seguono
- se il punto materiale non incontra nessuna altra radice di
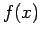 , ovviamente minore di
, ovviamente minore di 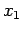 , prosegue percorrendo tutto l'asse
, prosegue percorrendo tutto l'asse 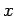 negativo senza mai fermarsi e da questo momento il moto diventa aperiodico (retrogrado) come nel caso 1.1;
negativo senza mai fermarsi e da questo momento il moto diventa aperiodico (retrogrado) come nel caso 1.1;
- se il punto materiale incontra la radice multipla
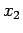 , ovviamente
, ovviamente 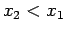 , allora tende asintoticamente alla posizione di ascissa
, allora tende asintoticamente alla posizione di ascissa 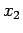 , come nel caso 1.2.1;
, come nel caso 1.2.1;
- infine se il punto materiale incontra la radice semplice
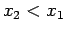 allora si ritorna al caso 1.2.2, cioè di nuovo si inverte il moto. Più precisamente dop aver raggiunto
allora si ritorna al caso 1.2.2, cioè di nuovo si inverte il moto. Più precisamente dop aver raggiunto 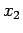 all'istante
con
all'istante
con
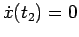 , il punto riparte con velocità positiva (riprende a percorrere l'asse
, il punto riparte con velocità positiva (riprende a percorrere l'asse 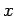 nel verso positivo) e ripassa dalla posizione iniziale
nel verso positivo) e ripassa dalla posizione iniziale 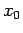 ad un istante
ad un istante 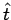 con velocità uguale alla velocità iniziale:
Assumendo ora
con velocità uguale alla velocità iniziale:
Assumendo ora 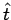 come istante iniziale il teorema di unicità del moto (Teorema di Cauchy 2.1), fissate le condizioni iniziali
come istante iniziale il teorema di unicità del moto (Teorema di Cauchy 2.1), fissate le condizioni iniziali
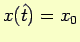 ,
,
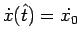 , il punto ripete lo stesso tipo di moto che ha effettuato nell'intervallo
, il punto ripete lo stesso tipo di moto che ha effettuato nell'intervallo
![$ [t_0,\hat{t}]$](img353.png) . Dunque il moto risulta periodico nell'intervallo
. Dunque il moto risulta periodico nell'intervallo ![$ [x_1,x_2]$](img354.png) : il punto "`fa la spola"' indefinitamente fra i due punti
: il punto "`fa la spola"' indefinitamente fra i due punti 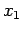 e
e 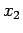 . Il periodo
. Il periodo 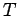 del moto sarà dato dalla somma del tempo
del moto sarà dato dalla somma del tempo 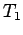 impiegato per andare da
impiegato per andare da 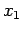 a
a 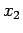 e del tempo
e del tempo 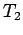 impiegato per ritornare da
impiegato per ritornare da 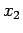 a
a 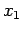 . Tenendo conto del fatto che nel primo tratto per andare da
. Tenendo conto del fatto che nel primo tratto per andare da 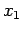 a
a 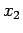 la velocità è negativa, mentre nel secondo tratto da
la velocità è negativa, mentre nel secondo tratto da 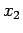 a
a 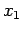 , la velocità è positiva, avremo:
, la velocità è positiva, avremo:
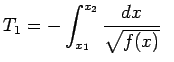
e
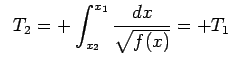
Pertanto
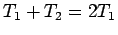 così che
che è un integrale generalizzato in entrambi gli estremi ma è finito poichè
così che
che è un integrale generalizzato in entrambi gli estremi ma è finito poichè 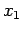 e
e 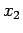 sono radici semplici di
sono radici semplici di 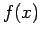 , per quanto visto precedentemente.
, per quanto visto precedentemente.
Abbiamo così concluso lo studio del moto nel caso di
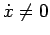 , vediamo ora il caso in cui
, vediamo ora il caso in cui 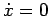 .
.
Caso 2
Il punto materiale ha velocità iniziale nulla, 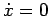 .
.
Essendo
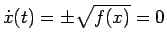 si avrà
e quindi
si avrà
e quindi 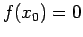 , cioè all'istante iniziale
, cioè all'istante iniziale 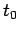 il punto si trova in una posizione da ascissa
il punto si trova in una posizione da ascissa 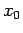 coincidente con uno degli zeri di
coincidente con uno degli zeri di 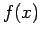 .
.
Il moto del punto per 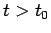 dipende dal valore di
dipende dal valore di
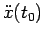 e abbiamo due sottocasi:
e abbiamo due sottocasi:
- 2.1
-
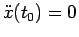 ,
,
- 2.2
-
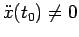 .
.
Caso 2.1
Se
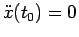 , cioè il punto materiale ha un'accelerazione iniziale nulla, l'equazione di Newton 2.1 sarà
, cioè il punto materiale ha un'accelerazione iniziale nulla, l'equazione di Newton 2.1 sarà
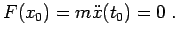 |
(3.12) |
Dalla 3.12 segue che l'equazione del moto
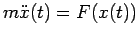 ammette come unica soluzione
ammette come unica soluzione 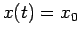 ,
,
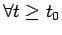 , soddisfacente i dati iniziali
, soddisfacente i dati iniziali
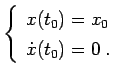 |
(3.13) |
Dunque il punto rimane immobile in 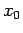 ad ogni istante successivo a quello iniziale, e
ad ogni istante successivo a quello iniziale, e 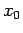 è una configurazione di equilibrio secondo la seguente definizione.
è una configurazione di equilibrio secondo la seguente definizione.
Definizione 3.1
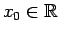 si dice configurazione di equilibrio se, posto il punto materiale in
si dice configurazione di equilibrio se, posto il punto materiale in 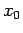 all'istante
all'istante 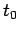 con velocità nulla, ivi rimane ad ogni istante successivo.
con velocità nulla, ivi rimane ad ogni istante successivo.
In base a quanto ottenuto sopra possiamo enunciare il seguente teorema.
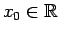 è una configurazione di equilibrio se e solo se
è una configurazione di equilibrio se e solo se
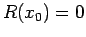
, o equivalentemente,
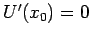
.
Caso 2.2
Se
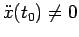 , cioè il punto materiale ha un'accelerazione non nulla, si metterà in moto con velocità positiva (moto diretto) se
, cioè il punto materiale ha un'accelerazione non nulla, si metterà in moto con velocità positiva (moto diretto) se
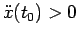 e con velocità negativa (moto retrogrado) se
e con velocità negativa (moto retrogrado) se
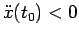 .
.
Dimostriamo questa affermazione nel caso
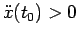 . Nell'altro caso si procede in modo analogo.
. Nell'altro caso si procede in modo analogo.
Essendo
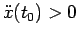 ,
,
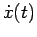 è crescente in
è crescente in 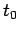 perciò
perciò
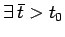 tale che
tale che
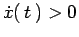 ,
,
![$ \forall t\in ]t_0,\bar{t}[$](img383.png) .
.
Ne segue che esiste
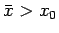 t.c.
Allora, poichè la funzione
t.c.
Allora, poichè la funzione 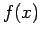 non si annulla nell'intervallo
non si annulla nell'intervallo
![$ ]x_0,\bar{x}[$](img386.png) possiamo calcolare il tempo
possiamo calcolare il tempo 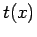 impiegato dal punto a raggiungere la posizione
impiegato dal punto a raggiungere la posizione
![$ x \in ]x_0,\bar{x}[$](img387.png) mediante l'integrale
mediante l'integrale
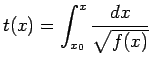 |
(3.14) |
che è un integrale generalizzato in 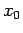 .
.
Tuttavia 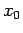 è una radice semplice di
è una radice semplice di 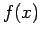 , poichè dalla 3.10 si ha
siccome per ipotesi
, poichè dalla 3.10 si ha
siccome per ipotesi
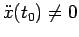 .
.
Allora, procedendo come nel caso 1.2.2 si ottiene che l'integrale 3.14 è convergente. Pertanto il punto impiega un tempo finito a raggiungere qualunque posizione 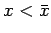 . Poichè per
. Poichè per
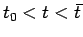 la velocità
la velocità
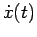 è non nulla, si può prender una qualunque di queste posizioni
è non nulla, si può prender una qualunque di queste posizioni 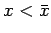 come configurazione iniziale, con corrispondente velocità iniziale diversa da zero, e da questo istante per lo studio qualitativo del moto si può ripartire esattamente dal Caso 1.
come configurazione iniziale, con corrispondente velocità iniziale diversa da zero, e da questo istante per lo studio qualitativo del moto si può ripartire esattamente dal Caso 1.
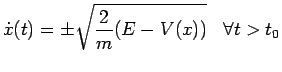
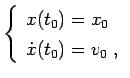
![]() determina il fatto che all'istante
determina il fatto che all'istante ![]() il moto sia diretto (nel verso positivo dell'asse
il moto sia diretto (nel verso positivo dell'asse ![]() ) o retrogrado (nel verso negativo di
) o retrogrado (nel verso negativo di ![]() ). Possiamo dunque orientare l'asse
). Possiamo dunque orientare l'asse ![]() in modo che sia
in modo che sia
![]() .
.![]() tale che
tale che
![]() ,
,
![]() .
.
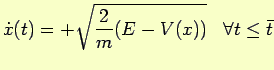 .
.
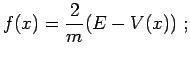 quindi
quindi
![]() non può essere negativa, gli intervalli di
non può essere negativa, gli intervalli di ![]() in cui il moto è consentito sono quelli per cui si ha
in cui il moto è consentito sono quelli per cui si ha
![]() , ossia
, ossia
![]() .
.
![]() nel piano
nel piano ![]() e la retta orizzontale
e la retta orizzontale ![]() : le regioni ammissibili di
: le regioni ammissibili di ![]() saranno quelle dove il grafico di
saranno quelle dove il grafico di ![]() sta al di sotto della retta
sta al di sotto della retta ![]() e tali tratti saranno finiti o infiniti a seconda che il corrispondente intervallo di
e tali tratti saranno finiti o infiniti a seconda che il corrispondente intervallo di ![]() sia finito oppure no.
sia finito oppure no.
![]() distinguiamo ora i casi:
distinguiamo ora i casi:
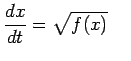 cioè
cioè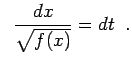
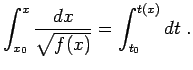
![]() in un tempo finito più o meno lungo; si ha infatti di nuovo
in un tempo finito più o meno lungo; si ha infatti di nuovo
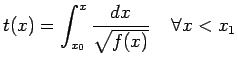
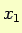 come radice di
come radice di ![]() radice dell' equazione
radice dell' equazione ![]() di molteplicità
di molteplicità ![]() , ovviamente
, ovviamente ![]() ,
, ![]() . Poichè
. Poichè
![]() per ipotesi possiamo allora scrivere
per ipotesi possiamo allora scrivere ![]() nella seguente forma:
nella seguente forma:
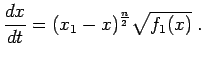
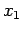 , a cui il punto si avvicina sempre più senza mai raggiungerlo.
, a cui il punto si avvicina sempre più senza mai raggiungerlo.
![]() radice semplice dell'equazione
radice semplice dell'equazione ![]() , ciò significa che
, ciò significa che
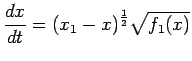
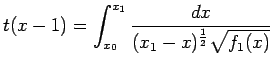
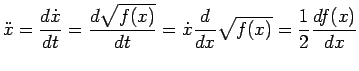
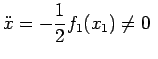 e in particolare
e in particolare 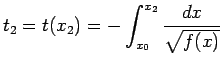
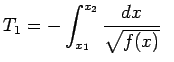 e
e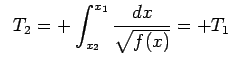
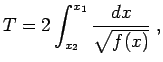
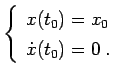
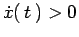 ,
,