Dimostrazione.
Si ha
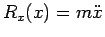
; moltiplichiamo per
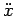
entrambi i membri ottenendo
dove
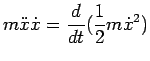
e
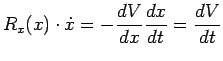
quindi avremo
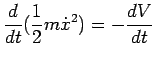
cioè
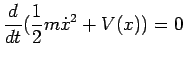
.
Vale perciò il teorema di conservazione dell'energia.
Vediamo ora il viceversa.
A partire da
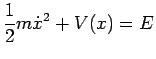
, deriviamo rispetto a
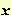
entrambi i membri ottenendo
dove
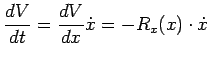
.
Quindi avremo
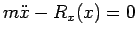
cioè
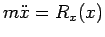
.
Troviamo così la
2.13

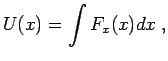
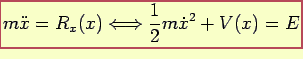
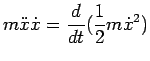 e
e
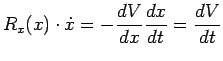
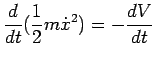
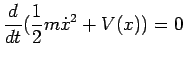 .
.
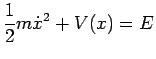 , deriviamo rispetto a
, deriviamo rispetto a 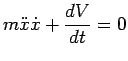
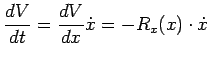 .
.
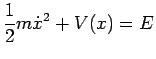 con
con