Sezione: Dinamica del punto materiale


Legge fondamentale della Dinamica
(II legge di Newton)

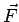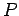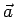Sia $ \vec{F}$ il vettore risultante di tutte le forze che agiscono su un punto materiale $ P$ e $ \vec{a}$ l' accelerazione di 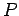$ P$ allora si ha:

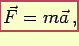$\displaystyle \vec{F}=m\vec{a}\,,$ (2.1)

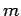dove $ m$ è un coefficiente positivo, detto massa del punto, che dipende solo dalla natura della materia di cui è costituito il punto e dall' unità di misura.

La 2.1 è equivalente a 3 equazioni scalari:

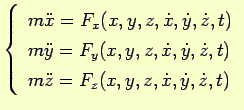$\displaystyle \left\{\begin{array}{ll} m\ddot{x}=F_x(x,y,z,\dot{x},\dot{y},\d... ...z},t)\\ m\ddot{z}=F_z(x,y,z,\dot{x},\dot{y},\dot{z},t)\\ \end{array}\right.$ (2.2)

Allora le 2.2 costituiscono un sistema di tre equazioni differenziali del secondo ordine in forma normale; esse però non determinano in modo univoco il moto del punto materiale, se non sono conosciuti ulteriori elementi; così per la risoluzione del sistema occorrono le cosiddette condizioni iniziali che dovranno sempre supporsi associate ad esso.
Esse consistono nell' assegnare, in un certo istante che potremo sempre assumere come origine del tempo, la posizione e la velocità del punto materiale. Cioè, occorre siano note, per 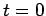$ t=0$, le coordinate 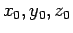$ x_0, y_0, z_0$ del punto e le componenti 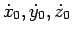$ \dot{x}_0,\dot{y}_0,\dot{z}_0$ della sua velocità.
Questo segue dal Teorema di Cauchy di cui ricordiamo l' enunciato.

Teorema 2.1 (di Chauchy)
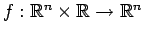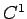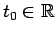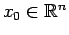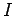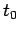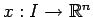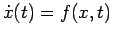
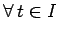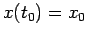  Sia $ f:\mathbb{R}^n\times\mathbb{R}\rightarrow\mathbb{R}^n$ di classe $ C^1$ e siano $ t_0\in\mathbb{R}$, $ x_0\in\mathbb{R}^n$ fissati. Allora esiste un intorno $ I$ di $ t_0$ ed una sola funzione $ x:I\rightarrow\mathbb{R}^n$ che soddisfi l' equazione differenziale $ \dot{x}(t)=f(x,t)$ $ \forall\,t\in I$ e la condizione $ x(t_0)=x_0$.

Ricordiamo che l'equazione differenziale

$\displaystyle \dot{x}=f(x,t)$

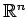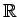in $ \mathbb{R}^n$ corrisponde ad un sistema di n-equazioni differenziali in $ \mathbb{R}$:
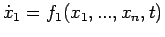
$ \dot{x}_1=f_1(x_1,...,x_n,t)$
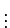
$ \vdots$
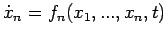
$ \dot{x}_n=f_n(x_1,...,x_n,t)$
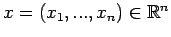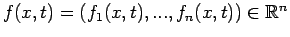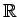con $ x=(x_1,...,x_n)\in\mathbb{R}^n$ , $ f(x,t)=(f_1(x,t),...,f_n(x,t))\in\mathbb{R}^n$. Come è noto ogni equazione differenziale del secondo ordine di forma normale in $ \mathbb{R}$:

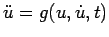$\displaystyle \ddot{u}=g(u,\dot{u},t)$ (2.3)

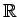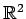è equivalente ad un sistema di due equazioni differenziali del primo ordine in $ \mathbb{R}$, ovvero ad una equazione differenziale del primo ordine in $ \mathbb{R}^2$.
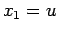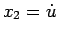Ponendo infatti $ x_1=u$ e $ x_2=\dot{u}$, la 2.3 diventa equivalente a:

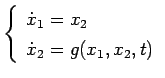$\displaystyle \left\{\begin{array}{ll} \dot{x}_1=x_2 \\ \dot{x}_2=g(x_1,x_2,t) \\ \end{array}\right.$ (2.4)

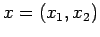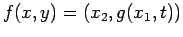Ponendo poi $ x=(x_1,x_2)$ e $ f(x,y)=(x_2,g(x_1,t))$, la 2.4 può essere riscritta in forma compatta:

$\displaystyle \ddot{x}=f(x,\dot{x},t)$

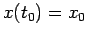La condizione iniziale $ x(t_0)=x_0$ diventa:

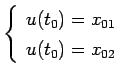$\displaystyle \left\{\begin{array}{ll} u(t_0)=x_{01} \\ u(t_0)=x_{02} \\ \end{array}\right.$ (2.5)

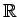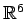Più in generale il sistema 2.2 equivale ad un sistema di 6 equazioni differenziali del I ordine in $ \mathbb{R}$ (cioè una equazione differenziale del I ordine in $ \mathbb{R}^6$).
La condizione iniziale imposta dal Teorema di Chauchy per garantire l' unicità della soluzione, diventa una condizione su 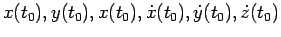$ x(t_0),y(t_0),x(t_0),\dot x(t_0),\dot y(t_0),\dot z(t_0)$, cioè sulla posizione e sulla velocità iniziali di $ P$.
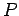Dal punto di vista dinamico la risoluzione della 2.2 garantisce la determinazione del moto del punto 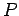$ P$, cioè delle sue coordinate:

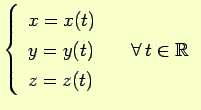$\displaystyle \left\{\begin{array}{lll} x=x(t) \\ y=y(t)\qquad\forall \,t\in\mathbb{R}\\ z=z(t) \\ \end{array}\right.$ (2.6)

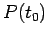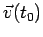a patto di conoscere il dato iniziale, cioè $ P(t_0)$ e $ \vec{v}(t_0)$, e le forze che agiscono sul punto stesso, di cui 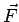$ \vec{F}$ è il vettore risultante.

Il lavoro La forza