Sezione: Analisi qualitativa dei moti unidimensionali nel piano delle fasi

Analisi qualitativa dei moti unidimensionali nel piano delle fasi

L'ambiente ideale per studiare il moto di un generico sistema unidimensionale è il piano delle fasi, cioè il piano $ (x,\dot{x})$.
Fissato il dato iniziale $ (x(0)=x_0,\dot{x}(0)=\dot{x_0})$ e quindi l'energia totale

$\displaystyle E=\frac{1}{2}m\dot{x_0}^2+V(x_0)$ (4.1)

lo scopo è quello di disegnare nel piano $ (x,\dot{x})$ la curva di equazioni parametriche

$\displaystyle \left\{\begin{array}{l} x=x(t) \\ \dot{x}=\dot{x}(t) \;,\;\;\forall t\in \mathbb{R}\\ \end{array}\right.$ (4.2)

detta curva di livello corrispondente al livello di energia $ E$. Più precisamante il procedimento è il seguente.

SCHEMA

  1. Si individuano i range dei valori che può assumere l'energia totale $ E$, detti livelli energetici (o livelli di energia), che in generale è dato dal seguente insieme

    $\displaystyle \Psi=\left\{E\in\mathbb{R}:E\geq \mbox{inf}_{x\in\mathbb{R}}V(x)\right\}\;,$ (4.3)

    come nell'Osservazione 3.2.


  2. Si fissa un valore arbitrario di $ E\in \Psi$ e in corrispondenza ad esso si individuano gli intervalli dell'asse reale $ x$ ammissibili come configurazioni per il punto materiale durante il suo moto a seguito di opportune condizioni iniziali compatibili col valore di $ E$, cioè soddisfacenti la 4.1.
    Indichiamo con $\mathbb{R}_E$ l'unione di questi intervalli. Tali intervalli saranno determinati dalla condizione

    $\displaystyle V(x)\leq E\;\;\;\;\forall x\in\mathbb{R}$

    come già fatto notare in Osservazione 3.2.
    Dal punto di vista grafico queste regioni si ottengono tracciando innanzitutto il grafico della funzione energia potenziale $ V(x)$ e quello della funzione energia totale $ E$ che corrisponde alla retta orizzontale $ y=E$, limitando l'analisi ai valori di $ x$ in cui il grafico di $ V$ non supera la retta $ y=E$ (come abbiamo visto negli esempi 3.1 e 3.2).


  3. Si fissa un valore arbitrario $ x_0 \in\mathbb{R}_\epsilon$ e si studia il moto che fa seguito ad un dato iniziale con $ x(0)=x_0$ e di energia totale $ E$. In base alla discussione alla Weierstrass precedentemente illustrata il moto potrà essere essenzialmente di quattro tipi.

    a.
    Punto fisso se $ x_0$ è una configurazione di equilibrio ed $ E=V(x_0)$. In questo caso le 4.2 diventano

    $\displaystyle \left\{\begin{array}{l} x(t)=x \\ \dot{x}(t)=0 \;,\;\;\forall t\in \mathbb{R}\\ \end{array}\right.$ (4.4)

    e la curva di livello si riduce ad un punto, $ (x_0,0)$ nel piano delle fasi $ (x,\dot{x})$.
    Dal Teorema 3.1 segue che le configurazioni di equilibrio corrispondono ai punti di stazionarietà del potenziale, cioè ai valori $ x_0$ tali che $ V'(x_0)=0$.
    b.
    Supponiamo sia $ x_0\in\,[x_1,x_2]$, essendo $ x_1$ e $ x_2$ radici semplici della funzione $ f(x)=E-V(x)$,tali che $ f(x)\neq 0$, $ \forall x\in\,]x_1,x_2[$.
    Allora il moto è periodico, cioè il punto oscilla fra $ x_1$ e $ x_2$. Quando il punto si muove da $ x_1$ a $ x_2$ il moto è diretto, quindi $ \dot{x}>0$.
    Pertanto la curva di livello corrispondente sarà una curva che connette i due punti $ x_1$ e $ x_2$ nel semipiano superiore dello spazio delle fasi come in figura 4.1.
    Figura 4.1: La freccia indica il verso di percorrenza della curva
    Image per1y
    Viceversa, quando il punto si muove da $ x_2$ a $ x_1$, il moto è retrogrado,cioè $ \dot{x}<0$.
    Dunque la curva di livello corrispondente sarà una curva che connette $ x_2$ e $ x_1$ nel semipiano inferiore dello spazio delle fasi come in figura 4.2.
    Figura 4.2: La freccia indica il verso di percorrenza della curva
    Image per2y
    In definitiva, la curva di livello completa sarà un'orbita chiusa passante per i due punti $ (x_1,0)$ e $ (x_2,0)$ e percorsa in senso orario.
    Figura 4.3: La curva è chiusa
    Image pertotale
    c.
    Supponiamo che $ x_0\in\,]x_1,x_2[$ dove $ x_2$ è una radice multipla di $ f(x)$, $ x_1$ è una radice semplice di $ f(x)$ oppure $ x_1=-\infty $, e $ f(x)\neq 0$, $ \forall x\in\,]x_1,x_2[$. (La discussione procede in maniera analoga se, viceversa, $ x_1$ è radice multipla e $ x_2$ semplice di $ f(x)$, oppure entrambe sono radici multiple).
    Nel caso in cui $ x_1$ è radice semplice di $ f(x)$, se $ \dot{x_0}>0$ il moto è asintotico verso $ x_2$ e la curva di livello corrispondente è del tipo disegnato in figura 4.4.
    Figura 4.4: Il tratteggio sta ad indicare che il punto si avvicina sempre più ad $ x_2$ senza mai raggiungerlo
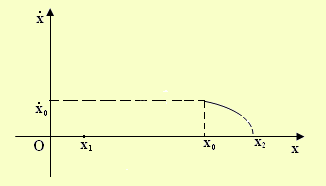
    Image radsempli
    Da osservare che il punto $ x_2$ non appartiene alla curva di livello in esame.
    Se $ \dot{x_0}<0$, allora il punto si dirige verso $ x_1$ dove si ferma e torna indietro muovendosi di moto diretto e asintotico verso $ x_2$ (come in fig.4.5).
    Figura 4.5: Il punto ha velocità iniziale negativa
    Image radsempli2
    La curva di livello che corrisponde a tutti i possibili dati iniziali compatibili con le ipotesi fatte su $ x_1$ e $ x_2$ e con $ x_0\in\,]x_1,x_2[$ sarà del tipo come in figura 4.6.
    Figura 4.6: Il punto ha velocità iniziale negativa
    Image radsemplitot
    Nel caso in cui $ x_1=-\infty $ e $ x_2$ è radice multipla di $ f(x)$ si hanno due possibilità: se $ \dot{x_0}>0$ di nuovo il moto è asintotico e diretto verso $ x_2$ e la curva di livello è ancora come in figura 4.4.
    La curva di livello completo corrispondente ad ogni velocità iniziale $ \dot{x_0}>0$ è data come in figura 4.7
    Figura 4.7: Il punto ha velocità iniziale positiva
    Image radinfiy
    Se invece $ \dot{x_0}<0$, allora il moto è aperiodico retrogrado e il punto percorre tutto l'asse $ x$ negativo senza mai fermarsi. La curva di livello è come in figura 4.8
    Figura 4.8: Il punto ha velocità iniziale negativa e $ x_1=-\infty $
    Image radmolti
    Vale la pena di osservare che se entrambe le radici sono multiple la curva di livello presenta due andamenti asintotici, uno verso $ x_1$ e l'altro verso $ x_2$.
    Si tratta di un'orbita limitata simile a quella della fig.4.3, privata dei due punti $ (x_1,0)$ e $ (x_2,0)$.
    Figura 4.9: $ x_1$ e $ x_2$ sono due radici multiple di $ f(x)$
    Image tendetot
    d.
    Supponiamo che $ x_0\in\,]-\infty,x_1]$ dove $ x_1$ è una radice semplice di $ f(x)$ (discussione analoga se $ x_0\in\,[x_1,+\infty[$) e $ f(x)\neq 0$, $ \forall x\in\,]-\infty,x_1[$.
    Se $ x_0>0$ il punto raggiunge $ x_1$ in un tempo finito, si ferma e riparte percorrendo tutto l'asse $ x$ negativo con moto retrogrado.
    Se $ x_0<0$ il punto procede immediatamente di moto retrogrado senza fermarsi mai.
    In entrambi i casi il moto è aperiodico e la curva di livello è come in figura 4.10.
    Figura 4.10: $ x_1$ radice semplice e $ x_2=-\infty $
    Image apetot
    Come abbiamo già osservato le radici multiple si hanno solo in corrispondenza a punti di stazionarietà di $ V(x)$ e quindi a configurazioni di equilibrio.


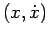
Osservazione 4.1   E' importante nel disegnare le curve di livello nel piano $ (x,\dot{x})$, avere presente che tali curve sono sempre a due a due disgiunte, cioè non hanno punti di intersezione, in virtù del teorema di Cauchy, cioè dell'unicità del moto che fa seguito ad un dato iniziale fissato.

Esempi Discussione alla Weierstrass