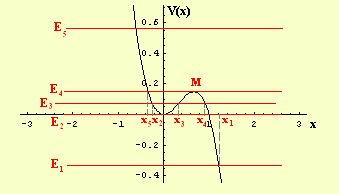
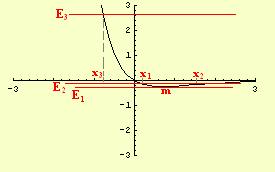
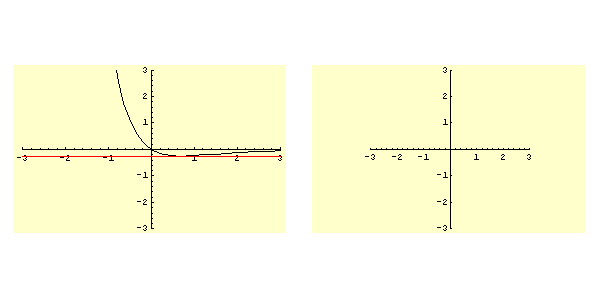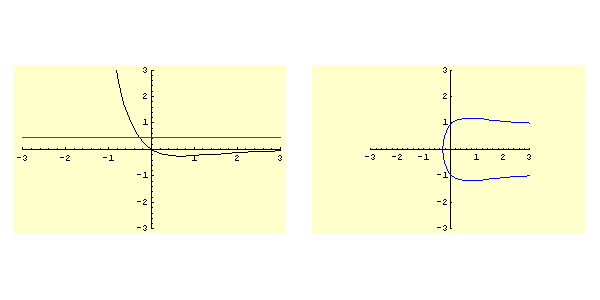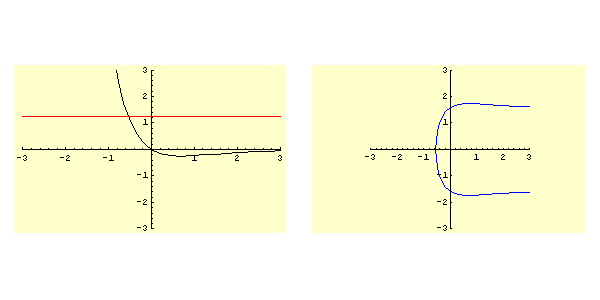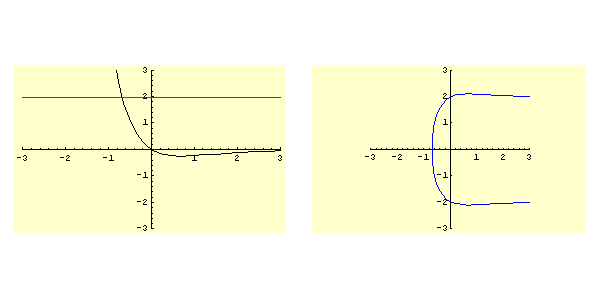
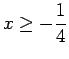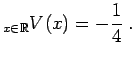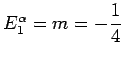Lo studio della funzione ![]() determina il grafico rappresentato in figura 5.1. In particolare si ha:
determina il grafico rappresentato in figura 5.1. In particolare si ha:
lim![]()
lim![]()
Inoltre si ha un minimo relativo in ![]() , con
, con
![]() , un massimo relativo in
, un massimo relativo in
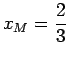 , con
, con
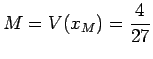 , e un flesso obliquo in
, e un flesso obliquo in
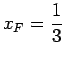 .
.
Infatti
![]() . Dunque gli unici punti di stazionarietà di
. Dunque gli unici punti di stazionarietà di ![]() , cioè le configurazioni di equilibrio si hanno per
, cioè le configurazioni di equilibrio si hanno per ![]() (equilibrio stabile) e per
(equilibrio stabile) e per
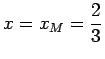 (equilibrio instabile).
(equilibrio instabile).
Ora, seguendo lo schema illustrato nel capitolo precedente, l'insieme ![]() (definito dalla 4.3) dei valori che può assumere l'energia totale
(definito dalla 4.3) dei valori che può assumere l'energia totale ![]() coincide con
coincide con
![]() in quanto
in quanto
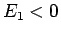 .
.
Come si evince immediatamente dalla figura 5.1 i soli valori ammisibili per il dato iniziale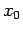 sono quelli dell'intervallo
sono quelli dell'intervallo
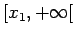 . Quindi si applica direttamente il punto 3d dello schema e il moto è sempre aperiodico e la corrispondente curva di livello nel piano
. Quindi si applica direttamente il punto 3d dello schema e il moto è sempre aperiodico e la corrispondente curva di livello nel piano
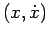 è quella contrassegnata dalla lettera
è quella contrassegnata dalla lettera 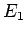 .
.
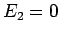 .
.
Si hanno due possibilità per il dato iniziale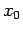 :
:
- (i)
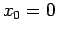 , corrispondente al caso 3a dello schema. In corrispondenza a questa configurazione di equilibrio stabile, l'orbita nel piano
, corrispondente al caso 3a dello schema. In corrispondenza a questa configurazione di equilibrio stabile, l'orbita nel piano
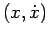 si riduce al punto
si riduce al punto 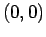 .
.
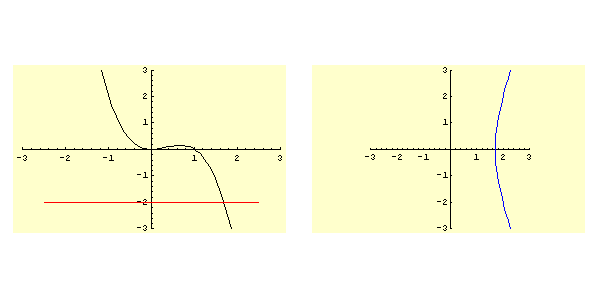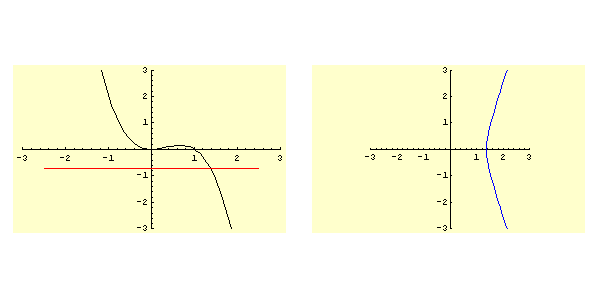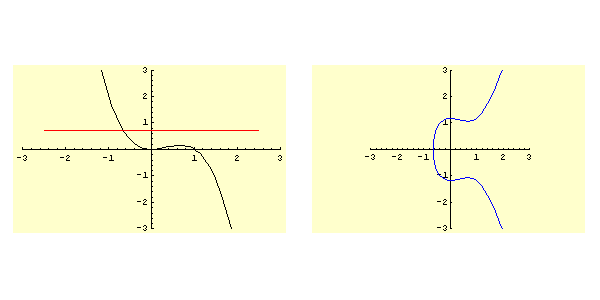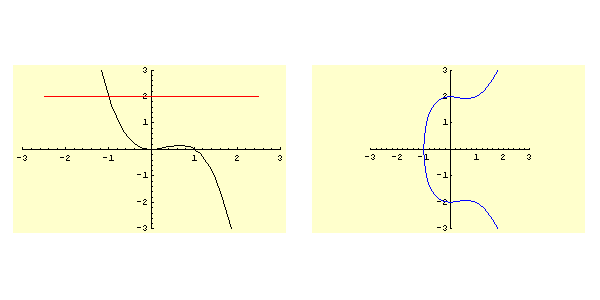
- (ii)
-
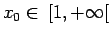 . Caso analogo al 1, cioè (3d dello schema): moto aperiodico con orbita determinata da
. Caso analogo al 1, cioè (3d dello schema): moto aperiodico con orbita determinata da 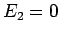 .
.
-
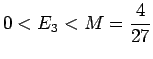 si hanno due possibilità:
si hanno due possibilità:
- (i)
-
![$ x_0\in\,]x_2,x_3[$](img440.png) (si veda figura 5.3).
(si veda figura 5.3).
Siamo nel caso 3b dello schema, pertanto il moto è periodico fra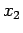 e
e 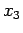 e l'orbita nel piano delle fasi è chiusa e percorsa in senso orario.
e l'orbita nel piano delle fasi è chiusa e percorsa in senso orario.
- (ii)
-
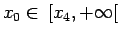
Di nuovo siamo nel caso 3d dello schema, analogo a 1: moto aperiodico.
-
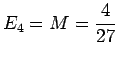
- (i)
-
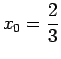 .
.
E' il caso 3a: configurazione di equilibrio instabile. Orbita in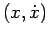 che si riduce al punto
che si riduce al punto
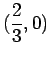 .
.
- (ii)
-
![$ x_0=]x_5,\displaystyle\frac{2}{3}[$](img446.png) .
.
E' il caso 3c: moto asintotico verso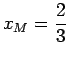 . Orbita come in figura 4.6, limitata non chiusa (manca il punto
. Orbita come in figura 4.6, limitata non chiusa (manca il punto
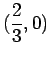 ) percorsa in senso orario.
) percorsa in senso orario.
- (iii)
-
![$ x_0=]\displaystyle\frac{2}{3},+\infty[$](img447.png) .
.
Caso 3c dello schema: se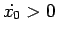 il moto è aperiodico; se
il moto è aperiodico; se
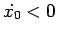 il moto è asintotico verso
il moto è asintotico verso
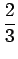 .
.
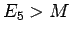 .
.
Siamo di nuovo nel caso 3d con moto aperiodico. In questo caso l'orbita subisce "`strozzature"' per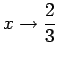 poichè la velocità tende ad un minimo relativo, dato che l'energia totale resta fissa mentre l'energia potenziale
poichè la velocità tende ad un minimo relativo, dato che l'energia totale resta fissa mentre l'energia potenziale 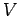 tende al suo massimo relativo.
tende al suo massimo relativo.
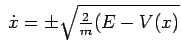
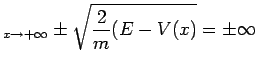
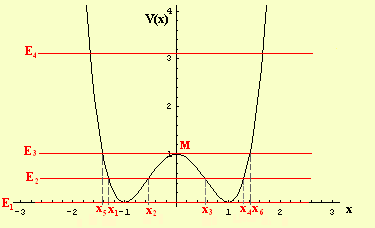
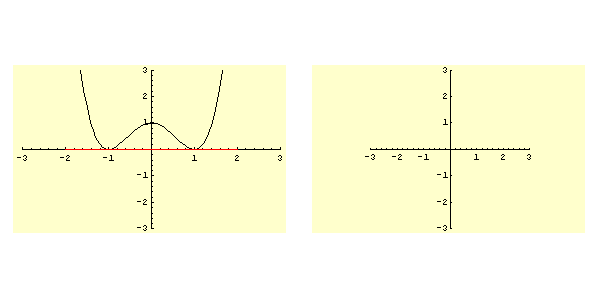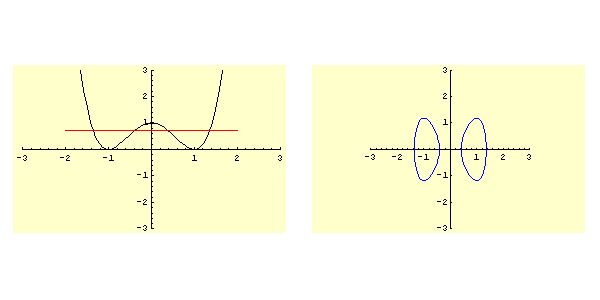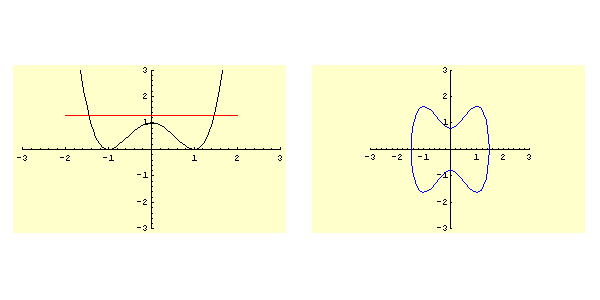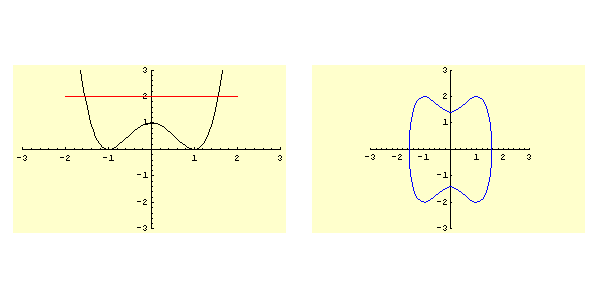
Lo studio della funzione ![]() determina il grafico rappresentato in figura 5.3. In particolare si ha:
determina il grafico rappresentato in figura 5.3. In particolare si ha:
![]()
![]()
Inoltre si hanno due minimi relativi in ![]() e
e ![]() , con
, con
![]() , un massimo relativo in
, un massimo relativo in ![]() , con
, con
![]() , e due flessi obliqui. Infatti
, e due flessi obliqui. Infatti
![]() .
.
Dunque gli unici punti di stazionarietà di ![]() , cioè le configurazioni di equilibrio si hanno per
, cioè le configurazioni di equilibrio si hanno per
![]() ,
,
![]() (equilibrio instabile) e per
(equilibrio instabile) e per ![]() (equilibrio instabile).
Ora, seguendo lo schema dell'analisi qualitativa, l'insieme dei valori ammissibili
(equilibrio instabile).
Ora, seguendo lo schema dell'analisi qualitativa, l'insieme dei valori ammissibili ![]() dell'energia totale
dell'energia totale ![]() coincide con
coincide con
![]() in quanto
in quanto
Passando al punto 2 dello schema, osserviamo che i valori di
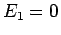 .
.
Si hanno due possibilità per il dato iniziale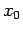 :
:
- (i)
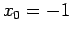 , corrispondente al caso 3a dello schema. In corrispondenza a questa configurazione di equilibrio stabile, l'orbita nel piano
, corrispondente al caso 3a dello schema. In corrispondenza a questa configurazione di equilibrio stabile, l'orbita nel piano
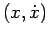 si riduce al punto
si riduce al punto 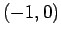 .
.
- (ii)
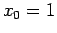 , analogo ad
, analogo ad 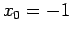 , ma con la differenza che ora l'orbita nel piano
, ma con la differenza che ora l'orbita nel piano
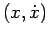 si riduce al punto
si riduce al punto 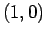 .
.
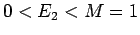
Si hanno due possibilità (vedi figura 5.3):- (i)
-
![$ x_0\in]x_1,x_2[$](img477.png)
Siamo nel caso 3b dello schema, pertanto il moto è periodico fra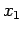 e
e 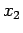 e l'orbita nel piano delle fasi è chiusa e percorsa in senso orario.
e l'orbita nel piano delle fasi è chiusa e percorsa in senso orario.
- (ii)
-
![$ x_0\in]x_3,x_4[$](img478.png)
Di nuovo siamo nel caso 3b, ma ora il moto è periodico fra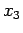 e
e 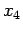 .
.
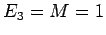
- (i)
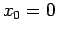 , siamo nel caso 3a dello schema: configurazione di equilibrio instabile. L'orbita nel piano delle fasi si riduce al punto
, siamo nel caso 3a dello schema: configurazione di equilibrio instabile. L'orbita nel piano delle fasi si riduce al punto 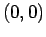 .
.
- (ii)
-
![$ x_0\in]x_5,1[$](img481.png) oppure
oppure
![$ x_0\in]1,x_6[$](img482.png) .
.
E' il caso 3c:moto asintotico verso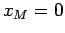 . Orbita come in figura 4.6, limitata, non chiusa (manca il punto
. Orbita come in figura 4.6, limitata, non chiusa (manca il punto 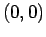 ) percorsa in senso orario.
) percorsa in senso orario.
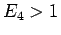
Siamo di nuovo nel caso3b: moto periodico e l'orbita nel piano delle fasi è chiusa, percorsa in senso orario.Osservazione 5.2 La curva di livello rappresentata in figura 5.4 viene disegnata in modo tale che in prossimità del punto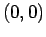 essa si "`schiaccia"'. Nel caso di
essa si "`schiaccia"'. Nel caso di 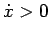 (
(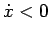 ) questo "`schiacciamento"' è dovuto al fatto che la velocità diminuisce (aumenta) in quanto legata all'energia potenziale e all'energia totale
) questo "`schiacciamento"' è dovuto al fatto che la velocità diminuisce (aumenta) in quanto legata all'energia potenziale e all'energia totale 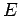 (in questo caso
(in questo caso 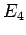 ) dalla legge
) dalla legge
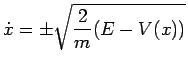 , dove
, dove 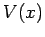 tende al suo punto di massimo relativo.
tende al suo punto di massimo relativo.
![]()