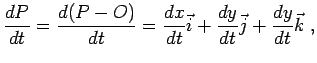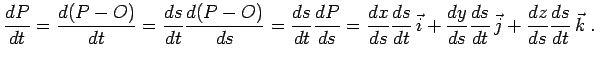Sezione: Elementi di calcolo vettoriale
Supponiamo di avere una funzione
 , cioè una legge che ad ogni
, cioè una legge che ad ogni
 associa uno e un solo vettore
associa uno e un solo vettore
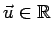 . Allora diremo che
. Allora diremo che
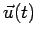 è un vettore varibile funzione di
è un vettore varibile funzione di 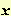 .
.
Naturalmente saranno funzioni di 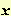 le 3 componenti
le 3 componenti
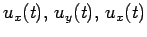 di
di
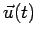 rispetto alla base
rispetto alla base
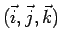 .
.
Poichè
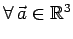 si ha che
si ha che
è immediato verificare che
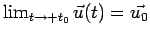 se e solo se
se e solo se
Possiamo ora definire la derivata di un vettore.
Dall'osservazione che segue la Definizione 1.8 si ha il seguente
Le componenti della derivata di un vettore, valgono le derivate delle sue componenti.
Osservazione
1.
3
Se il vettore 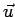 è costante in modulo, eventualmente variabile in direzione e verso, si ha
cioè la derivata di un vettore costante in modulo è perpendicolare al vettore stesso, se
è costante in modulo, eventualmente variabile in direzione e verso, si ha
cioè la derivata di un vettore costante in modulo è perpendicolare al vettore stesso, se
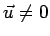 e
e
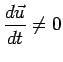 .
.
Se poi il vettore 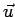 è funzione di una variabile numerica
è funzione di una variabile numerica 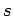 , a sua volta funzione della variabile
, a sua volta funzione della variabile 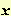 , sicchè
, sicchè 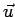 risulta funzione composta di
risulta funzione composta di 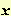 ,
,
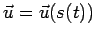 , si ha
, si ha
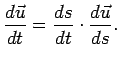 |
(1.2) |
Consideriamo ancora la variabile 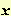 e supponiamo che ad ogni suo valore corrisponda la posizione di un punto
e supponiamo che ad ogni suo valore corrisponda la posizione di un punto 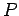 dello spazio.
dello spazio.
Diremo che il punto 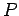 è funzione di
è funzione di 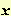 e scriveremo
Se
e scriveremo
Se  è un punto dello spazio non dipendente dal tempo, chiameremo derivata di
è un punto dello spazio non dipendente dal tempo, chiameremo derivata di 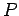 rispetto a
rispetto a 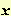 la derivata del vettore
la derivata del vettore 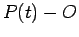 , e tale derivata non dipende da
, e tale derivata non dipende da 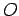 .
.
Se
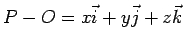 si ha
cioè le componenti della derivata di un punto sono le derivate delle sue coordinate.
Se poi
si ha
cioè le componenti della derivata di un punto sono le derivate delle sue coordinate.
Se poi 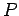 è funzione di un parametro
è funzione di un parametro 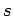 a sua volta funzione di
a sua volta funzione di 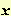 , si ha, per la 1.2,
Avendo introdotto la nozione di derivata di un punto possiamo ora parlare di velocità.
, si ha, per la 1.2,
Avendo introdotto la nozione di derivata di un punto possiamo ora parlare di velocità.
![]() si ha che
si ha che
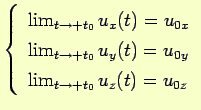
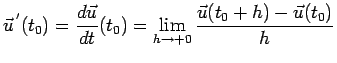
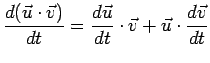 ;
;
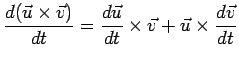 ;
;
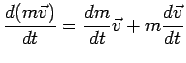 ,
,
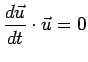
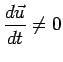 .
.
![]() è funzione di una variabile numerica
è funzione di una variabile numerica ![]() , a sua volta funzione della variabile
, a sua volta funzione della variabile ![]() , sicchè
, sicchè ![]() risulta funzione composta di
risulta funzione composta di ![]() ,
,
![]() , si ha
, si ha