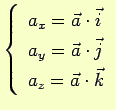Sezione: Elementi di calcolo vettoriale
Se
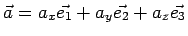 e
e
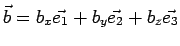 è facile verificare che
è facile verificare che
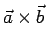 è dato dal seguente determinante:
è dato dal seguente determinante:
Nel seguito, per la base canonica
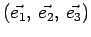 useremo la notazione più classica in Meccanica:
useremo la notazione più classica in Meccanica:
La terna
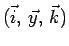 è una base ortonormale, cioè i vettori sono a due a due ortogonali e ciascuno di norma unitaria:
è una base ortonormale, cioè i vettori sono a due a due ortogonali e ciascuno di norma unitaria:
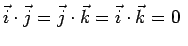
e
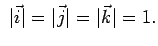
Da questo segue che se
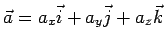 si ha
da cui si può scrivere
si ha
da cui si può scrivere
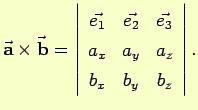
![]() useremo la notazione più classica in Meccanica:
useremo la notazione più classica in Meccanica: