Sezione: Elementi di calcolo vettoriale
Definizione 1.6
Una terna
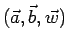 di vettori (linearmente indipendenti) si dice terna destra se, disponendo la mano destra in linea col vettore
di vettori (linearmente indipendenti) si dice terna destra se, disponendo la mano destra in linea col vettore 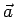 e facendola ruotare come per portare
e facendola ruotare come per portare 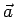 sopra
sopra 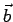 , il pollice teso punta nel verso di
, il pollice teso punta nel verso di 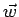 .
.
Dati due vettori 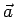 e
e 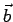 , che possiamo suppore di ugual origine
, che possiamo suppore di ugual origine 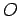 , si chiama prodotto vettoriale fra i due vettori
, si chiama prodotto vettoriale fra i due vettori 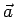 e
e 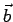 , e lo indicheremo col simbolo
, e lo indicheremo col simbolo
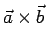 , il vettore
, il vettore 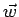 tale che:
tale che:
-
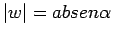 dove
dove 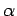 è l'angolo compreso fra i due vettori;
è l'angolo compreso fra i due vettori;
- la direzione è quella ortogonale al piano individuato da
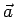 e
e 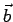 ;
;
- il verso è quello in cui
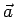 ,
,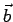 e
e 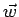 nell'origine formano una terna destra.
nell'origine formano una terna destra.
Ovviamente il prodotto vettoriale, a differenza del prodotto scalare, è un vettore.
Osservazione 1.2
Il prodotto vettoriale è nullo quando sono nulli o l'uno o l' altro dei vettori che lo costituiscono, o è nullo il seno dell'angolo 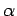 compreso fra essi, ossia quando i due vettori sono paralleli, poichè
compreso fra essi, ossia quando i due vettori sono paralleli, poichè
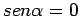 per
per 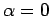 e
e
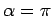 .
.
In particolare si ha
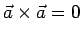
Il prodotto vettoriale non gode della proprietà commutativa infatti si ha
però gode della proprietà distributiva rispetto alla somma, cioè
inoltre in generale non gode della proprietà associativa.
![]() e
e ![]() , che possiamo suppore di ugual origine
, che possiamo suppore di ugual origine ![]() , si chiama prodotto vettoriale fra i due vettori
, si chiama prodotto vettoriale fra i due vettori ![]() e
e ![]() , e lo indicheremo col simbolo
, e lo indicheremo col simbolo
![]() , il vettore
, il vettore ![]() tale che:
tale che: