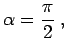Sezione: Elementi di calcolo vettoriale
Si può dimostrare la seguente disuguaglianza di Schwarz:
Ne segue che
Si pone per definizione:
da cui si può ricavare la rappresentazione intrinseca del prodotto scalare:
Definizione 1.5
Due vettori si dicono ortogonali se il loro prodotto scalare è nullo.
Allora, se 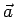 e
e 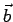 sono vettori non nulli,
sono vettori non nulli,
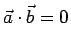
se e solo se
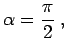
cioè due vettori sono ortogonali se e solo se i corrispondenti segmenti orientati formano un angolo di
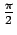 .
.
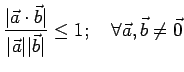
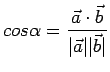
![]() e
e ![]() sono vettori non nulli,
sono vettori non nulli,