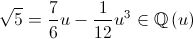Soluzione
7.
- Si
ha: u=√5-i
⇒ u2=5-1-2i√5
⇒ (u2-4)2=20i2
⇒ u4-8u2+16=-20
da
cui x4-8x2+36
è un polinomio a coefficienti razionali,
monico, irriducibile (vedi sotto) e che
si annulla in u, dunque è il polinomio minimo
di u su Q:
pu(x)=x4-8x2+36
Irriducibilità
di pu.
Il Δ del polinomio in x2
è negativo quindi non è un quadrato in Q: se ne deduce che pu
non fattorizza su Q
come (x2-a)(x2-b).
Potrebbe fattorizzare su Q
in più generali polinomi di secondo grado di tipo ax2+bx+c.
Poichè
in pu compaiono solo
potenze pari di x, se a
è una radice
lo è anche -a. Poichè pu
è un polinomio a coefficienti reali,
se a è una radice lo è
anche ā, cioè il complesso
coniugato
di a. Conosciamo una radice di pu,
cioè u=√5-i∈C\R, quindi u≠ū;
questo ci dà le quattro radici complesse di pu:
u, -u, ū,
-ū. Quindi su C pu=(x-u)(x+u)(x-ū)(x+ū)
e su R pu=(x2-2Re(u)x+∣u∣2)(x2+2Re(u)x+∣-u∣2)=(x2-2√5x+6)(x2+2√5x+6).
Ricordiamo
infatti che per ogni numero
complesso z si ha (x-z)(x-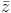 )=x2-2Re(z)x+∣z∣2∈R[x].
Poichè pu non
ha fattori
lineari su R
non ne ha neanche su Q
e se avesse fattori di secondo grado irriducibili questi sarebbero
anche fattori su R.
Quindi pu è
irriducibile.
)=x2-2Re(z)x+∣z∣2∈R[x].
Poichè pu non
ha fattori
lineari su R
non ne ha neanche su Q
e se avesse fattori di secondo grado irriducibili questi sarebbero
anche fattori su R.
Quindi pu è
irriducibile.
- Una base
di Q(u)
è data da: {1, u, u2, u3}={1,
√5-i, 4-2i√5, 2√5-14i} quindi:
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 8.

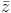 )=x2-2Re(z)x+∣z∣2∈R[x].
Poichè pu non
ha fattori
lineari su R
non ne ha neanche su Q
e se avesse fattori di secondo grado irriducibili questi sarebbero
anche fattori su R.
Quindi pu è
irriducibile.
)=x2-2Re(z)x+∣z∣2∈R[x].
Poichè pu non
ha fattori
lineari su R
non ne ha neanche su Q
e se avesse fattori di secondo grado irriducibili questi sarebbero
anche fattori su R.
Quindi pu è
irriducibile.