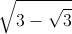pu(x)=x4-6x2+6
Irriducibilità
di pu. Primo modo.
Per il criterio
di Eisenstein, con p=2 (o p=3),
pu è
irriducibile.
Secondo modo.
Il discriminante del polinomio in x2
è pari a 12, non quadrato in Q: se ne deduce che pu
non fattorizza su Q
come prodotto di (x2-a)(x2-b).
Può fattorizzare su Q
in più generali polinomi di
secondo grado di tipo ax2+bx+c?
No infatti, dato che in pu
le potenze di x sono solo pari, si ha: pu(u)=0=pu(-u)
e: (x-u)(x+u)=x2-u2=x2-(3+√3)
e così deve risultare che, per qualche a
e b:
(x2-3-√3)(x2+ax+b)=x4-6x2+6
Se a
fosse diverso da 0, nel polinomio a primo membro comparirebbe un
monomio diverso da 0 di primo grado in x,
quindi a=0. Su R pu,
come polinomio in x2, ha
le due radici (entrambe maggiori di 0) x2=3±√3
quindi x4+6x2+6=(x2-(3+√3))(x2-(3-√3))
da cui su R:
Note ora le
quattro radici, tutte reali, di pu
si può valutare se esso è o meno irriducibile su Q.
Chiamati:
u1=u u2=-u u3=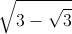 u4=-
u4=-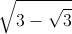
si ha che,
dei prodotti (x-u1)(x-u2),
(x-u1)(x-u3),
(x-u1)(x-u4),
nessuno ha coefficienti razionali e pertanto pu(x)
è irriducibile in Q[x].
Infatti pu
non si può scomporre su Q
nel prodotto di un polinomio lineare
per uno di terzo grado, essendo tutte le radici non razionali e non
si può scomporre su Q
come prodotto di due polinomi
irriducibili f e g di
secondo grado, perchè le possibilità per f
sono: f=(x-u1)(x-u2),
f=(x-u1)(x-u3),
f=(x-u1)(x-u4),
e nessuno dei tre come già detto è razionale.
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 7.

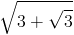 ⇒ u2=3+√3
⇒ u2-3=√3
⇒ (u2-3)2=3
⇒ u4-6u2+6=0
⇒ u2=3+√3
⇒ u2-3=√3
⇒ (u2-3)2=3
⇒ u4-6u2+6=0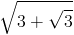 ⇒ u2=3+√3
⇒ u2-3=√3
⇒ (u2-3)2=3
⇒ u4-6u2+6=0
⇒ u2=3+√3
⇒ u2-3=√3
⇒ (u2-3)2=3
⇒ u4-6u2+6=0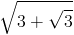 )(x+
)(x+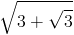 )(x-
)(x-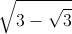 )(x+
)(x+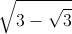 )
)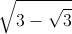 u4=-
u4=-