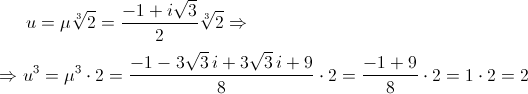
Si ha:
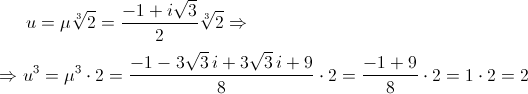
da cui il polinomio x3-2, che è il polinomio minimo di u su Q. Esso è infatti monico, ha coefficienti razionali, si annulla in u ed è irriducibile: ha infatti tre radici (una reale ∛2 e due complesse μ∛2 e μ2∛2, si veda sotto) di cui nessuna razionale e quindi non ha un fattore lineare in Q[x].
Quanto a μ esso è algebrico infatti, come si vede sopra, ha polinomio minimo x3-1: μ è una delle due radici cubiche complesse primitive dell'unità.
Torna agli esercizi.
Torna alla teoria.
Vai all'esercizio 28.
