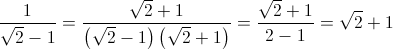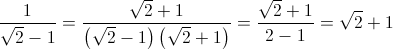Soluzione
26.
Si
ha:
- Si ha: u=1+√2
⇒ (u-1)2=2
⇒ u2-2u+1=2
⇒ u2-2u-1=0
x2-2x-1
è un polinomio a coefficienti interi quindi razionali, monico ed irriducibile (il discriminante Δ=8
non è un quadrato in Q)
che si annulla in u, dunque unico a soddisfare
tutti e quattro questi requisiti. Quindi:
pu=x2-2x-1∈Q[x]
è
il polinomio minimo
di u su Q.
- L'estensione
Q(u)/Q è finita in quanto
generata su Q
da un solo numero algebrico,
dunque è anche algebrica.
Il grado [Q(u):Q]
è pari al grado di pu
su Q e
cioè è pari a 2.
- Si ha che u=1+√2∈Q(v)
e v=√2∈Q(u),
perchè 1+√2=v+1 e √2=u-1.
Da qui le due inclusioni: Q(u)⊆Q(v)
e Q(v)⊆Q(u).
Ne segue dunque l'uguaglianza: Q(v)=Q(u).
- Il polinomio x2-2x-1
ha radici 1±√2∈Q(u)⊆R ma che non sono
razionali. Dunque tale polinomio è irriducubile su Q mentre spezza in
due fattori lineari x-1-√2
ed x-1+√2 su Q(u)
e su R. Si
ha allora che l'ideale I=(x2-2x-1)
è primo soltanto nell'anello di polinomi Q[x] e non in Q(u)[x]
ed in R[x];
infatti ad esempio in Q(u)[x]
si ha x-1-√2∉I,
x-1+√2∉I
ma (x-1-√2)(x-1+√2)∈I.
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 27.