Chiusura e derivato
Definizione 6.1
Sia S un sottoinsieme di X. Si chiama chiusura di S, e si denota con 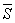 , il più piccolo chiuso contenente S (o, equivalentemente l’intersezione di tutti i chiusi che contengono S).
, il più piccolo chiuso contenente S (o, equivalentemente l’intersezione di tutti i chiusi che contengono S).
Esempio
 Osservazioni 6.2
Osservazioni 6.2
 S è chiuso Û
S è chiuso Û
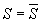

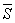 = X \ Est (S)
= X \ Est (S)
Dimostrazione
 Osservazione 6.3 Siano S e T sottoinsiemi di X:
Osservazione 6.3 Siano S e T sottoinsiemi di X:
- se S Í
T, si ha che
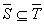 ;
;
 ;
;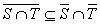 ;
;
Dimostrazione
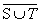
Esempio
Proposizione 6.4
Sia S Í
X; allora sono equivalenti:
- S è chiuso;
- S = Int (S) È
Fr (S);
- Fr (S) Í
S.
Dimostrazione
Esempio
Definizione 6.5
Sia S Í
X;
un punto x Î
X è detto aderente ad S se  ;
;
un punto x Î
X è detto di accumulazione per S se per ogni intorno U di x si ha
(U \ {x}) Ç
S ¹
Æ.
Si chiama derivato di S e si indica con D (S) l’insieme dei punti di accumulazione di S.
Esempio
Proposizione 6.6
Sia S Í
X, allora:
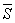 = S È
Fr (S);
= S È
Fr (S);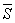 = S È
D (S).
= S È
D (S).
Dimostrazione
Esempio
Proposizione 6.7
Un punto x Î
X è aderente ad un sottoinsieme S di X Û
"
U intorno di x,
U Ç
S ¹
Æ
Dimostrazione
Definizione 6.8
Un sottoinsieme S di X si dice denso in X se  .
.

 Esempi Esempi |
 Esercizi Esercizi |
![]() Osservazioni 6.2
Osservazioni 6.2![]() S è chiuso Û
S è chiuso Û
![]()
![]()
![]() = X \ Est (S)
= X \ Est (S)
![]() Osservazione 6.3 Siano S e T sottoinsiemi di X:
Osservazione 6.3 Siano S e T sottoinsiemi di X:![]()

![]()
 Esempi
Esempi Esercizi
Esercizi