Esempi sulla Chiusura e il Derivato di un insieme

 

 

Esempio 1

 

Sia R con la topologia euclidea, consideriamo l'insieme S = { n Î N e n ¹ 0} allora la chiusura di S è:  ;

 

Dotiamo ora R della topologia cofinita, la chiusura di S è:  = R;

 

 

 

Esempio 2

 

Sia (R², e), consideriamo il disco aperto D_r((0,0)) = S:

la chiusura di S è:  = D_r((0,0))È{(x, y) | x²+y² = r2},

in pratica si tratta del disco unito alla circonferenza.

 

Osserviamo che spesso per indicare un disco col bordo troviamo la notazione: .

 

 

Esempio 3

 

Abbiamo visto che  ora vediamo qualche esempio in cui vale l'inclusione ma non l'uguaglianza:

  Consideriamo in R² con la topologia euclidea due dischi aperti presi in modo tale che le rispettive frontiere, cioè le circonferenze siano tangenti:

vediamo che SÇT = Æ, la cui chiusura è il Æ stesso,

mentre , quindi abbiamo che Æ = = {a};

   Sia R con la topologia euclidea e siano

S = { ; n Î N e n ¹ 0} e T = {- ; n Î N e n ¹ 0}, come nel caso precedente abbiamo che SÇT = Æ, ma quindi è evidente la disuguaglianza.

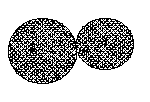
Vediamo un caso in cui invece vale l'uguaglianza:

consideriamo un qualsiasi insieme non vuoto X con la topologia discreta; sappiamo che ogni sottoinsieme di X è sia aperto che chiuso, sappiamo che la chiusura di un insieme chiuso è l'insieme stesso, quindi abbiamo  .

 

Attenzione! In generale non vale l'uguaglianza!

 

 

 

Esempio 4

 

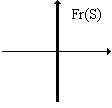
Consideriamo in (R²,e) consideriamo l'insieme S = {(x, y) | x £ 0};

allora:

Int(S) = {(x, y) | x < 0},

Fr(S) = {(x, y) | x = 0};

S = Int(S) È Fr(S) equivale a dire che S è chiuso.

 

 

 

 

Esempio 5

 

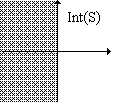Sia R con la topologia euclidea, consideriamo l'insieme S = { ; n Î N e n ¹ 0} allora il derivato di S è: D(S) = {0};

 

Dotiamo ora R della topologia cofinita, allora D(S) = R.

 

 

 

Esempio 6

 

Ogni sottoinsieme finito di R ha derivato vuoto e interno vuoto, quindi coincide con la sua frontiera.

 

 

 

Esempio 7

 

Consideriamo R con la topologia euclidea:

se a < b e S è uno qualsiasi degli intervalli (a, b], [a, b), [a, b], (a, b), allora Int(S) =(a, b), Fr(S) = {a, b}, D(S) = [a, b] e  = [a, b].

 

In R con la topologia cofinita gli insiemi chiusi sono gli insiemi finiti ed R stesso, quindi si ha che se prendiamo S come sopra:

 = R,

Int(S) = Æ,

Fr(S) = R.

 

 

 

Esempio 8

 

Vediamo alcuni esempi in cui vale = S È Fr(S) = S È D(S):

   riprendiamo l'esempio1: S = { ; n Î N e n ¹ 0} abbiamo visto che Fr(S) = SÈ{0}, D(S) = {0} e = SÈ{0} = S È Fr(S) = S È D(S).

   consideriamo in R con la topologia euclidea l'intervallo (a, b) = S, sappiamo che  Fr(S)={a, b} e D(S) = [a, b];  = [a, b] = SÈFr(S) = SÈD(S).

 

 

 

Esempio 9

 

L'insieme dei numeri razionali Q è denso in R, infatti la chiusura di Q è R.

 

 

 

Esempio 10

 

Riprendiamo l'esempio7: sia R con la topologia cofinita e S uno degli intervalli definiti sopra; abbiamo visto che  = R, quindi in questo caso, gli intervalli sono densi in R.