massimo e di minimo
Il massimo e il minimo vengono spesso detti anche massimo assoluto o minimo assoluto
si dice che x0ÎDf è un punto di massimo (minimo) locale o relativo per la funzione f se esiste un intorno Ix0 di x0 tale che:
f(x)
 f(x0) )
f(x0) )
 x Î Ix0
x Î Ix0
 Df
Df
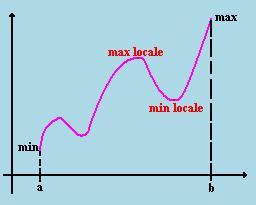
Nei punti di massimo o minimo locali di una funzione derivabile che siano interni al dominio la derivata è nulla.
Per trovare i massimi e minimi prendiamo in considerazione:
1) tutti i punti massimi e minimi locali, dove f'(x0)=0 ;
2) eventuali punti angolosi;
3) estremi dell'intervallo.
Confrontandoli troviamo così il massimo e minimo assoluto.
CONDIZIONE NECESSARIA
Se f(x) è derivabile , affinchè un punto sia di massimo o di minimo locale deve essere: f'(x)=0
Dunque si tratterà di risolvere tale equazione per determinare possibili punti di massimo o di minimo locale.
I valori xi che la soddisfano sono solo probabili punti di massimo o minimo locale, in quanto potrebbero anche essere punti di flesso.
I punti in cui si annulla la derivata prima si dicono punti stazionari o punti critici.
Per sapere se questi sono punti di massimo di minimo per la curva si può procedere in 2 modi:
| 1°METODO: | Si studia il segno della derivata prima, studiando la disequazione f'(x)>0 Il calcolo della derivata prima serve per determinare gli intervalli in cui la funzione cresce o decresce, facendoci comprendere se i punti trovati sono di massimo o di minimo. I punti di massimo sono quelli t.c. f'(xi)=0 mentre f'(x)>0 a sinistra di xi e f'(x)<0 a destra; I punti di minimo sono quelli t.c. f'(xi)=0 con f'(x)<0 a sinistra di xi e ,f'(x)>0 a destra. Invece se la derivata nell'intorno di tali punti non cambia di segno, questi non sono nè di massimo nè di minimo. |
| 2°METODO: | Si sostituiscono le ascisse dei punti xi nella derivata seconda e si guarda il segno che questa assume. Il calcolo della derivata seconda serve per determinare gli intervalli in cui la curva è concava o convessa: se f''(xi)>0 allora la concavità sarà rivolta verso l'alto perciò il punto è di minimo ; se f''(xi)<0 allora la concavità sarà rivolta verso il basso perciò il punto è di massimo; se f''(xi)=0 allora non possiamo concludere nulla. |
CALCOLO DELLE ORDINATE DEGLI EVENTUALI PUNTI DI MASSIMO E MINIMO LOCALE
Basta sostituire una alla volta le ascisse dei punti di massimo o di minimo nell'equazione della curva e ricavare l'ordinata.
E' utile riportare con un segno i risultati sul grafico.
OSSERVAZIONI
1) Se si somma una costante alla funzione y=f(x)
 la funzione y=f(x)+c ha negli stessi punti x i massimi e i minimi assoluti.
la funzione y=f(x)+c ha negli stessi punti x i massimi e i minimi assoluti.2) Se si moltiplica per una costante positiva y=f(x)
 la funzione y=cf(x) ha negli stessi punti x i massimi e i minimi assoluti.
la funzione y=cf(x) ha negli stessi punti x i massimi e i minimi assoluti.3) Se f(x)>0 per qualsiasi xÎI e consideriamo y=1/f(x)
 la funzione y=f(x) ha il massimo assoluto dove
y=1/f(x) ha il minimo assoluto e viceversa.
la funzione y=f(x) ha il massimo assoluto dove
y=1/f(x) ha il minimo assoluto e viceversa.4) Se e solo se f(x)>0
 xÎI
si ha che y=f(x)
e y=[f(x)]n hanno negli stessi punti x i massimi e i minimi assoluti.
xÎI
si ha che y=f(x)
e y=[f(x)]n hanno negli stessi punti x i massimi e i minimi assoluti.
 Esempi
Esempi
 Esercizi
Esercizi


