Sia dato un punto x0Î
 xÎI
xÎI
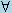 xÎI
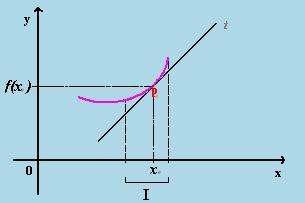
xÎIPer definizione i punti di flesso sono quei punti in cui la curva cambia concavità passando da concava a convessa (o viceversa) con continuità;
di conseguenza la funzione f''(x) passerà da un valore positivo ad uno negativo (o viceversa) con continuità quindi per il teorema dei valori intermedi ci sarà un punto in cui f''(x) =0
a.Se f''(x0)>0 la funzione è convessa in x0;
b.Se f''(x0)<0 la funzione è concava in x0;
c.Se f''(x0) =0 e f'''(x0) ¹0 la curva ha nel punto P0(x0,f(x0)) un flesso.
a.Se in x0Î]a,b[ f'(x0) =0 e f''(x0) =0 e f'''(x0)>0 allora x0 è un punto di flesso ascendente
b.Se in x0Î]a,b[ f'(x0) =0 e f''(x0) =0 e f'''(x0)<0 allora x0 è un punto di flesso discendente
Basta sostituire una alla volta le ascisse dei punti di flesso nell'equazione della curva e ricavare l'ordinata corrispondente.
Nell'ipotesi che sia
f''(x0) = f'''(x0) = ... = f (n-1)(x0) = 0 e f n(x0)¹0
si possono presentare i seguenti casi:
a. n pari, f n(x0)>0 allora f è convessa in x0;
n pari, f n(x0)<0 allora f è concava in x0;
b. n dispari, allora la funzione ha un flesso nel punto di ascissa x0.
Se nel punto x0Î]a,b[ sono veificate le seguenti condizioni:
f'(x0) = f''(x0) = ... = f (n-1)(x0) =0 e f n(x0)¹0
si avrà uno dei seguenti casi:
a.se n è pari, f n(x0)>0 allora il punto x0 è di minimo locale;
se n è pari, f n(x0)<0 allora il punto x0 è punto di massimo locale;
a.se n è dispari, f n(x0)>0 allora il punto x0 è ascissa di un punto di flesso a tangente orizzontale ascendente;
se n è dispari, f n(x0)<0 allora il punto x0 è ascissa di un punto di flesso a tangente orizzontale discendente.
Tale metodo consiste nel calcolare le soluzioni dell'equazione f'(x) =0 e,indicate con x0 una di esse,nel calcolare poi la derivata seconda f''(x).
Si possono presentare allora i seguenti casi:
| METODO DELLE DERIVATE SUCCESSIVE | |
| 1°CASO: f''(x0)¹0 |
allora x0 è un punto di massimo o minimo locale a seconda che sia
f''(x0)<0 o f''(x0)>0 |
| 2°CASO: f''(x0) =0 |
in tal caso si calcola la derivata terza f'''(x0); se poi
f'''(x0) ¹0, allora x0 è ascissa di un punto di flesso a tangente orizzontale
ascendente o
discendente a seconda che risulti f'''(x0)>0 o f'''(x0)<0
. Se invece anche f'''(x0) =0 si passa a calcolare le derivate successive in x0. Il procedimento si arresta se si incontra una derivata che non si annulla in x0. Se essa è di ordine pari si cadrà nel 1°CASO, mentre se è di ordine dispari avremo un flesso (come per f'''(x0) ¹0). |
 Esempio Esempio
|
|
 Esercizi
Esercizi


