7. Associazione fra caratteri quantitativi |
| |
|
|
| |
Esaminiamo ora in dettaglio l'associazione fra due caratteri quantitativi.
Introduciamo alcune nozioni preliminari. |
| |
Definizione 32. Data la distribuzione unitaria doppia di due caratteri X e Y quantitativi, si definisce baricentro la coppia 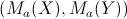 data dalle medie aritmetiche dei due caratteri. data dalle medie aritmetiche dei due caratteri. |
| |
Definizione 33. A partire dalla distribuzione unitaria doppia di due caratteri quantitativi X e Y osservati su un collettivo di n unità, si definisce grafico di dispersione l'insieme 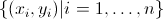 delle coppie di modalità
dei due caratteri osservate per ogni unità del collettivo. Tali coppie possono
essere rappresentate come punti di un piano cartesiano i cui assi corrispondono ai due caratteri e in cui l'origine viene poi traslata in corrispondenza
del baricentro. delle coppie di modalità
dei due caratteri osservate per ogni unità del collettivo. Tali coppie possono
essere rappresentate come punti di un piano cartesiano i cui assi corrispondono ai due caratteri e in cui l'origine viene poi traslata in corrispondenza
del baricentro. |
| |
A partire dal grafico di dispersione si parla di concordanza se la maggior
parte degli scostamenti dalla media è concorde, cioè se la maggior parte dei
punti del grafico di dispersione appartiene al I e III quadrante. Al contrario,
si parla di discordanza se la maggior parte degli scostamenti è discorde. |
| |
Esempio 34. |
|
| |
Il grafico di dispersione è di per sé molto utile per evidenziare se prevale la concordanza o la discordanza fra due caratteri. E'
possibile tuttavia
introdurre un indice che permette di effettuare la stessa analisi con un semplice calcolo, senza dover ricorrere al grafico di dispersione. Si tratta della
covarianza. |
| |
Definizione 35. A partire dalla distribuzione unitaria doppia, la covarianza tra due caratteri quantitativi è definita come la media dei prodotti
degli scostamenti delle variabili X e Y dalle rispettive medie: |
| |
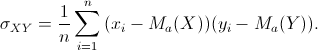
|
(11) |
| |
Il prodotto  è detto codevianza. è detto codevianza. |
|
| |
Si può dimostrare facilmente la seguente |
|
| |
Proposizione 36. La covarianza verifica le seguenti proprietà. |
|
| |
1.
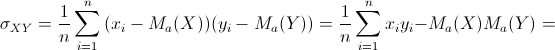

|
(12) |
| |
2. Se due caratteri sono statisticamente indipendenti allora la loro covarianza è nulla.
3. Indicando con  e e  le deviazioni standard di X e Y si ha le deviazioni standard di X e Y si ha |
| |
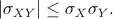 |
(13) |
| |
Inoltre  se e solo se esiste un legame perfetto di tipo
lineare tra X e Y, ossia se e solo se esiste un legame perfetto di tipo
lineare tra X e Y, ossia 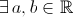 tali che Y=a+bX. tali che Y=a+bX. |
| |
Dimostrazione.  |
|
| |
Per la proprietà 2 della Proposizione 36 non vale il viceversa. Si possono
infatti fornire semplici controesempi. |
| |
Esempio 37. |
|
| |
Un difetto della covarianza è quello di dipendere dall'unità di misura delle
osservazioni cosicché non è corretto confrontare il valore della covarianza calcolato su diverse distribuzioni doppie. Per ovviare tale problema è necessario
introdurre un indice relativo. |
| |
Definizione 38. Si definisce coefficiente di correlazione lineare di
Bravais e Pearson l'indice, atto a misurare l'interdipendenza lineare tra due
caratteri, dato da: |
| |
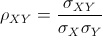 |
(16) |
| |
Dalla Proposizione 36 segue immediatamente il seguente |
|
| |
Corollario 39. Il coefficiente di correlazione lineare gode delle seguenti
proprietà:
1. 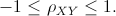
2. 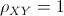 oppure oppure 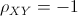 se e solo se tra i due caratteri sussiste un
perfetto legame lineare del tipo Y=a+bX. In particolare, per b<0 si ha se e solo se tra i due caratteri sussiste un
perfetto legame lineare del tipo Y=a+bX. In particolare, per b<0 si ha 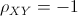 e per b>0 si ha e per b>0 si ha 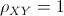 . .
3. se e solo se se e solo se 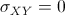 , il che può essere dovuto all'indipendenza dei due
caratteri oppure a qualche relazione di tipo non lineare (in quest'ultimo
caso i due caratteri vengono detti incorrelati). , il che può essere dovuto all'indipendenza dei due
caratteri oppure a qualche relazione di tipo non lineare (in quest'ultimo
caso i due caratteri vengono detti incorrelati).
4. Dati 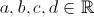 e due caratteri quantitativi X e Y, si costruiscono le
trasformazioni lineari e due caratteri quantitativi X e Y, si costruiscono le
trasformazioni lineari 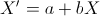 e e 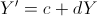 . Per il coefficiente
di correlazione tra X' e Y' si ha . Per il coefficiente
di correlazione tra X' e Y' si ha
 se i coefficienti b e d hanno stesso segno; se i coefficienti b e d hanno stesso segno;
 in caso contrario. in caso contrario.
In particolare, se come trasformazione lineare consideriamo proprio la
standardizzazione dei caratteri: 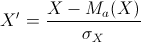 e e  si ha
quindi che si ha
quindi che  . . |
| |
|
 |
|
 |
|
 |
 |
|
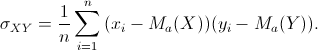
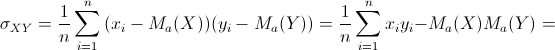
![]()
![]()
![]() oppure
oppure ![]() se e solo se tra i due caratteri sussiste un
perfetto legame lineare del tipo Y=a+bX. In particolare, per b<0 si ha
se e solo se tra i due caratteri sussiste un
perfetto legame lineare del tipo Y=a+bX. In particolare, per b<0 si ha ![]() e per b>0 si ha
e per b>0 si ha ![]() .
.![]() se e solo se
se e solo se ![]() , il che può essere dovuto all'indipendenza dei due
caratteri oppure a qualche relazione di tipo non lineare (in quest'ultimo
caso i due caratteri vengono detti incorrelati).
, il che può essere dovuto all'indipendenza dei due
caratteri oppure a qualche relazione di tipo non lineare (in quest'ultimo
caso i due caratteri vengono detti incorrelati).![]() e due caratteri quantitativi X e Y, si costruiscono le
trasformazioni lineari
e due caratteri quantitativi X e Y, si costruiscono le
trasformazioni lineari ![]() e
e ![]() . Per il coefficiente
di correlazione tra X' e Y' si ha
. Per il coefficiente
di correlazione tra X' e Y' si ha![]() se i coefficienti b e d hanno stesso segno;
se i coefficienti b e d hanno stesso segno;![]() in caso contrario.
in caso contrario.![]() e
e ![]() si ha
quindi che
si ha
quindi che ![]() .
.

