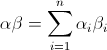. Essa dice che se 
e 
sono due vettori
in , se con 
indichiamo il loro prodotto scalare e con 
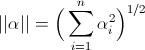e 
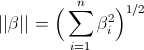le loro rispettive norme, vale la seguente
disuguaglianza:La dimostrazione di 1 e 2 è piuttosto semplice e si basa
sulle proprietà della media aritmetica. Per ragioni di brevità ci limitiamo a
dimostrare la proprietà 3, utilizzando la disuguaglianza di Cauchy-Schwarz
in . Essa dice che se e sono due vettori
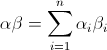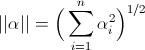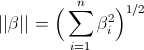in , se con indichiamo il loro prodotto scalare e con e le loro rispettive norme, vale la seguente
disuguaglianza:
Inoltre l'uguaglianza:
|
(14)
(15) |
vale se e solo se 
e 
sono linearmente indipendenti, cioè 
tale che 
, ovvero 
.
Ponendo ora 
e 
dalla (14) si ottiene:
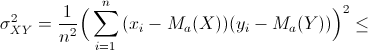
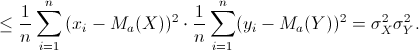
Da cui risulta: 
Inoltre l'uguaglianza vale se e solo se tale che
ovvero se e solo se 
, da cui Y=a+bX con 
e b=t.
CVD
