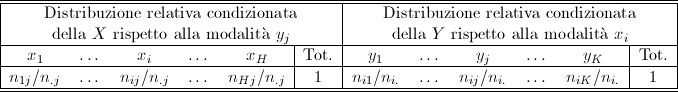5. Frequenze congiunte e tabelle a doppia entrata
     
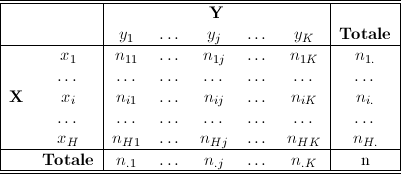
  Procediamo ora all'analisi congiunta di due caratteri X e Y osservati su uno stesso collettivo di n unità. Se da un lato possiamo utilizzare la distribuzione unitaria doppia, come definita nella Definizione 10, dall'altro risulta essere molto utile un tipo di rappresentazione più sintetica come la distribuzione di frequenze congiunte attraverso la tabella a doppia entrata.
 

Definizione 20. Dati due caratteri X e Y, rispettivamente con H e K modalità e , definiamo tabella a doppia entrata la Tabella 6 il cui corpo centrale è costituito da una matrice di ordine HxK il cui generico elemento , per e , rappresenta la frequenza congiunta, ossia la frequenza assoluta delle unità che presentano congiuntamente la modalità di X e la modalità di Y.

La colonna e la riga dei totali sono dette distribuzioni marginali e corrispondono esattamente alle distribuzioni di frequenze semplici dei due caratteri. In particolare, la colonna del totale è la distribuzione semplice del carattere X e il generico termine indica la frequenza assoluta delle unità che presentano la modalità ; analogamente la riga del totale indica la distribuzione semplice del carattere Y e il generico termine indica la frequenza assoluta delle unità che presentano la modalità .
 
  Tabella 6: Tabella a doppia entrata
  Definizione 21. Le righe e le colonne interne alla tabella a doppia entrata identificano le cosiddette distribuzioni condizionate. In particolare, facendo riferimento alla Tabella 6, si consideri la distribuzione data dalla generica riga i-esima: . Essa è detta distribuzione condizionata della Y rispetto alla modalità di X.
  Osservazione 3. In una tabella a doppia entrata riferita a due caratteri rispettivamente con H e K modalità, osservati su un collettivo di n unità, è immediato verificare le seguenti relazioni:
 

(10)
  Definizione 22. Anche nel caso delle tabelle a doppia entrata si può parlare di frequenze relative o percentuali, dove il generico elemento interno alla tabella a doppia entrata è espresso, rispettivamente, da e da . La distribuzione marginale relativa di X si ottiene come per e fornisce la distribuzione di frequenze relative semplici del carattere X. Lo stesso vale per il carattere Y, per il quale la distribuzione marginale relativa si ottiene come per .
 

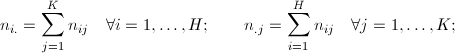
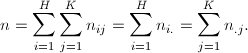
Definizione 23. La distribuzione relativa condizionata di X rispetto alla modalità di Y si ottiene come
Viceversa la distribuzione relativa condizionata di Y rispetto alla modalità di X si ottiene come
Queste distribuzioni vengono anche dette rispettivamente profili colonna e profili riga della tabella a doppia entrata e possono essere rappresentate come in Tabella 7.
 
  Tabella 7: Profili colonna e profili riga
  Esempio 24.