Osservazione 16   Sia  una permutazione di . La relazione  definita da

è una relazione di equivalenza nell’insieme .

Infatti la relazione  gode delle seguenti proprietà:

-         riflessiva: , cioè ;

-         simmetrica: se  allora , cioè se  allora ;

-         transitiva: se  e  allora ,   cioè se  e  allora .

Tale relazione induce una partizione di  in sottoinsiemi disgiunti.

 

Definizione 17   Se  e , si chiama orbita di  la classe di equivalenza di  secondo la relazione di equivalenza :

.

 

Esempio 18   In  sia . L’orbita dell’elemento 3 è l’insieme

.

Infatti

 

Proposizione 19   Se  e , esiste un intero positivo  minimo tale che , e l’orbita di  è l’insieme

.

 

Dimostrazione.   L’insieme  è non vuoto, infatti:

l’orbita di  è contenuta in , quindi gli , al variare di , non possono essere tutti distinti; sia quindi

, con

da cui

cioè

, con .

Sia allora  il più piccolo intero positivo tale che .

Proviamo innanzi tutto che se  è un intero, .

Si ha

,

da cui segue

.

Inoltre gli elementi dell’insieme  sono tutti distinti. Infatti se esistessero , tali che  si avrebbe . Ma essendo  il più piccolo intero positivo tale che , necessariamente , cioè .

□

 

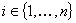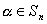Osservazione 20   Siano  e . L’orbita di  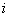è 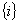 se e solo se .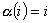