Definizione 10   Sia , con , un sottoinsieme di . La permutazione  di  tale che:

-          se ;

-         ;

-         ,

è chiamata ciclo di lunghezza k, e viene indicata con .

 

Esempio 11   In  il ciclo  rappresenta la permutazione

;

osserviamo che tale permutazione è rappresentata anche dai cicli , , .

Si può però dimostrare la seguente

 

Proposizione 12   Un ciclo si scrive in modo unico come , con .

 

Osservazione 13   Per vedere come agisce il ciclo , si possono disporre i  interi, , su un cerchio, come in figura, e così osservare che   manda ogni intero su questo cerchio nel successivo intero sul cerchio, nella direzione indicata dalla freccia:

 

 

 

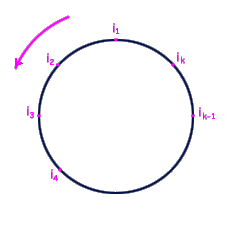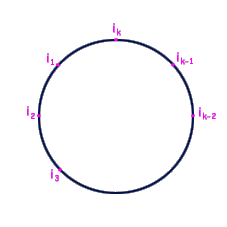
In altre parole l’azione di  su , consiste in una rotazione di , in senso antiorario, del cerchio su se stesso.

Se  è un ciclo, poniamo ; si ha:

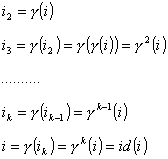
quindi .

Definizione 14   Se  e  sono due cicli di , si dice che  e  sono cicli disgiunti se .

 

Osservazione 15   Se  e  sono due cicli disgiunti di , allora , cioè il prodotto di cicli disgiunti è commutativo.

 

Dimostrazione.   Sia . Si hanno le seguenti possibilità:

-         : ;

-          e quindi : , in quanto ;

-          e quindi : .

In ogni caso si ottiene .

□