Proposizione 1   Sia  un insieme non vuoto. L’insieme

con l’operazione di composizione è un gruppo.

 

Dimostrazione.   Per ogni si ha:

-         , cioè la composizione di due applicazioni biunivoche è ancora un’applicazione biunivoca;

-         la composizione è associativa, cioè .

     Notiamo dapprima che le scritture  hanno senso; inoltre  si ha:

      e

      cioè

;

-         la funzione identità su , , è l’elemento neutro di : infatti  si ha

;

-         l’applicazione inversa di , , è l’inverso di  in :

.

□

 

Definizione 2   Sia 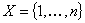. Il gruppo  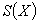è detto gruppo simmetrico su n lettere, ed è indicato con .

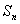Ogni elemento  di  viene chiamato permutazione, e viene denotato con

.

 

Esempio 3   In  la permutazione che manda  in ,  in ,  in  si scrive come

.