Geometria iperbolica > Teoremi e definizioni >Il biangolo
|
IL
BIANGOLO
|
| Vediamo
ora un teorema molto interessante, che possiamo considerare
l'analogo iperbolico del teorema
29 di Euclide, ovvero il primo di quelli dimostrati utilizzando
il V postulato.
Il teorema 29 trattava di ciò che Euclide chiamava
"una retta incidente su due parallele", che rappresentiamo
in forma tronca nella seguente figura:
|
 figura 1
figura 1
|
| Diamo
un nome alla corrispondente figura iperbolica.
|
DEFINIZIONE |
| |
Se dagli estremi
di un segmento di retta data, e da uno stesso lato vengono
tracciate due rette parallele asintoticamente l'una
all'altra nella direzione in cui si allontanano da essa,
la figura che ne risulta si dice biangolo, e il segmento
dato ne è la base. |
Esempi
|
XABY è
un biangolo. Ha solo due angoli, da cui il nome, poiché
i prolungamenti di AX e di BY non si incontrano
mai. AB è la base. |
|
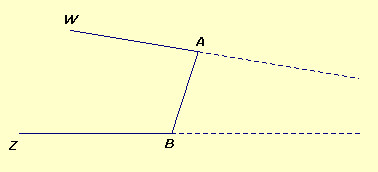
WABZ
non è un biangolo perché la direzione di parallelismo
è verso AB e non a partire da AB
come dovrebbe essere. |
. 
|
Confrontiamo le rette trasversali
euclidee con il biangolo iperbolico.
Se prolunghiamo la retta trasversale euclidea della figura1
otteniamo:
|
|
l'angolo a
è detto esterno e nel teorema 29 Euclide aveva
dimostrato che esso è uguale a b,
che è l'angolo interno e opposto.
Consideriamo ora invece il biangolo, cosa succede se ne prolunghiamo
in modo analogo la base AB? Cosa possiamo dire degli
angoli ^CBY, che chiamiamo esterno, e ^BAX,
che sarà il corrispondente angolo interno e opposto?
|
|
|
TEOREMA 8 |
| |
In un biangolo
un angolo esterno è maggiore dell'angolo interno
e opposto. |
|
| |
 |
 |