Geometria iperbolica > Teoremi e definizioni > Teoremi 27-29
di Euclide
|
|
TEOREMA 27 di Euclide |
| |
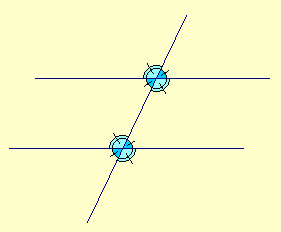
Se una retta
intersecando altre due rette forma con esse angoli alterni
interni uguali fra loro, le due rette saranno fra loro parallele. |
|
TEOREMA 28 di Euclide |
| |
Due rette sono
parallele se una terza retta che cada su di esse forma un
angolo esterno uguale all'angolo interno e opposto che è
dalla stessa parte, oppure forma angoli interni dalla stessa
parte la cui somma sia uguale a due retti. |
|
|
|
TEOREMA 27/28 di Euclide |
| |
Se, quando
due rette sono intersecate da una terza, sussiste tra gli
angoli una qualsiasi delle otto relazioni menzionate sopra,
le due rette sono parallele. |
NOTA
Questo problema può essere dimostrato senza ricorrere all'uso
del V postulato, fa dunque parte della geometria neutrale. |
| |
|
TEOREMA 29 di Euclide
(inverso del TEOREMA 27/28) |
| |
In un piano,
una retta che intersechi due rette parallele forma con esse
angoli alterni uguali fra loro, angoli esterni uguali agli
angoli interni e opposti, e dalla stessa parte angoli interni
la cui somma è uguale a due retti. |
|
NOTA
Questo è il primo teorema per la cui dimostrazione Euclide
ricorre all'utilizzo del V postulato, è dunque il primo vero
e proprio teorema di geometria euclidea. |
| |