|
Geometria iperbolica > Teoremi e definizioni > Le parallele
asintotiche
|
|
TEOREMA 4 |
| |
Se una retta
è asintoticamente parallela, in una direzione
data, ad un'altra retta, allora la seconda retta è
asintoticamente parallela alla prima nella stessa direzione. |
|
|
COROLLARIO |
| |
Se una retta
è parallela divergente ad un'altra retta, allora
la seconda retta è parallela divergente alla
prima. |
|
|
TEOREMA 5 |
| |
Se due rette
sono asintoticamente parallele, nella stessa direzione,
alla medesima retta, allora esse sono asintoticamente
parallele, in quella direzione, fra loro. |
|
|
TEOREMA 6 |
| |
Le parallele
asintotiche si avvicinano l'una all'altra nella direzione
del parallelismo. |
|
|
|
|
|
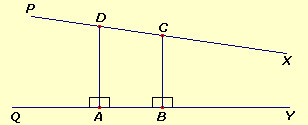
Dire che le due parallele asintotiche
si avvicinano l'una all'altra nella direzione del parallelismo
significa che il segmento di perpendicolare tracciato dall'una
all'altra si accorcia andando in quella direzione.
|
E' possibile dire di più,
cioè che le parallele asintotiche non solo si avvicinano
l'una all'altra ma, se prolungate nella direzione del parallelismo,
diventano arbitrariamente vicine.
Ovvero è possibile rendere la lunghezza BC tanto
piccola a piacere semplicemente scegliendo il punto B
abbastanza lontano verso destra; naturalmente, essendo PX
e QY parallele, BC non può mai diventare
uguale a zero.
Ecco perchè le rette asintotiche vengono chiamate così!
(Ricordiamo che in geometria analitica un asintoto di un grafico
di una funzione è una retta alla quale il grafico si
avvicina infinitamente senza mai raggiungerla.).
|
|
TEOREMA 7 |
| |
Data una qualunque
coppia di parallele asintotiche e una retta qualsiasi,
su ognuna delle due parallele (o eventualmente sul loro
prolungamento) esiste un punto tale che la perpendicolare
condotta da quel punto all'altra parallela (o al suo
prolungamento) è uguale alla retta data. |
|
|
| |
|
 |
 |