Geometria iperbolica > Teoremi e definizioni > Le parallele
asintotiche
|
Le parallele
asintotiche
|
| 
|
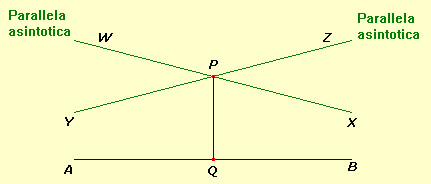
Possiamo
pensare che ciascuna delle parallele asintotiche punti in
una direzione particolare, che chiameremo "direzione
di parallelismo": per WPX la direzione di parallelismo
è da W verso X, e per YPZ
è da Z verso Y.
|
|
TEOREMA 2 |
| |
Le parallele asintotiche ad una
retta passanti per un punto formano angoli uguali e acuti
con la perpendicolare condotta dal punto alla retta. |
|
|
|
TEOREMA 3 |
| |
Se una retta è la parallela
asintotica per un punto dato, in una direzione data,
a una retta data, allora essa è, per ognuno dei
propri punti, la parallela asintotica nella direzione
data alla retta data. |
|
|
Supponiamo
che la direzione data sia verso destra. PX è
la parallela asintotica destra ad AB per P,
il teorema afferma che PX (o RX) è
la parallela asintotica destra anche per R.
|
|
COROLLARIO |
| |
Se una retta è per un punto
una parallela divergente a una retta data, allora essa
lo è anche per ciascuno dei propri punti. |
|
Il TEOREMA
3 ci esime dalla necessità di specificare un punto
particolare quando diciamo che una retta è parallela
asintotica ad un'altra, infatti questa sarà parallela
asintotica all'altra per ciascuno dei propri punti.
Analogamente il COROLLARIO ci dispensa dallo specificare un
punto particolare quando diciamo che una retta è parallela
divergente ad un'altra.
Possiamo concludere che la proprietà di parallelismo,
sia asintotico che divergente, è una proprietà
della retta globalmente intesa.
|
|
 |
 |