|
Geometria iperbolica > I modelli della geometria iperbolica>
Poincaré
|
Ultime
osservazioni
|
| Consideriamo la figura |
| 
|
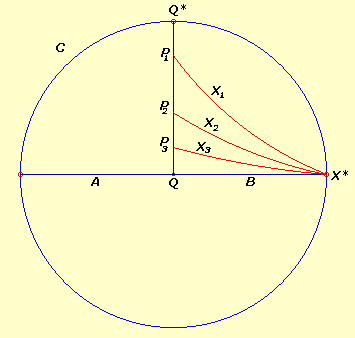
Q è
il centro di C, A e B
sono su un diametro e Q*Q è il semi-diametro
perpendicolare; P1, P2, P3,…,
sono punti su Q*Q, ognuno distante da Q la
metà del precedente (dal punto di vista di un osservatore
esterno); P1X1, P2X2,
P3X3,…, sono le corrispondenti
parallele asintotiche destre di AB (per chi sta all'interno
di C sono gli archi ortogonali che uniscono quei punti a X*).
Si osservi che gli angoli di parallelismo X1P1Q,
X2P2Q, X3P3Q,..,
diventano sempre più prossimi ad un angolo retto.
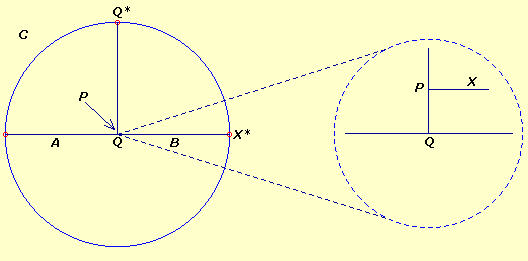
Continuando questa analisi, consideriamo
un punto P su Q*Q che sia vicinissimo a
Q, tanto che solo con un potentissimo microscopio
sia distinguibile da Q; in figura il cerchio tratteggiato
a destra rappresenta un ingrandimento della regione intorno
a Q.
|
| 
|
PX
è la parallela asintotica destra ad AB
(vale a dire l'arco ortogonale passante per P e X*):
l'angolo ^XPQ è estremamente prossimo ad un
angolo retto.
Supponiamo che
P sia così prossimo a Q che la differenza
fra l'angolo ^XPQ e un angolo retto non possa essere
rivelata dagli strumenti in possesso agli abitanti di C;
e che gli abitanti siano estremamente piccoli e vivano tutti
nelle vicinanze di Q e non abbiano mai raggiunto
e nemmeno visto col telescopio un punto più distante
di P da Q.
Abbiamo già osservato che la geometria all'interno
di C è quella iperbolica,
ma nella nostra discussione precedente avevamo tacitamente
ammesso che gli abitanti fossero abbastanza grandi rispetto
a C da accorgersene.
Con le ulteriori limitazioni che abbiamo imposto ora, gli
abitanti si trovano nella situazione descritta nel trattare
la "riconciliazione
col buon senso", e giudicheranno euclideo lo spazio
che li circonda; in realtà quello spazio è iperbolico,
ma essi non saranno in grado di scoprirlo perché sembrerà
loro che gli angoli di parallelismo siano sempre retti.
|
E
se noi fossimo una versione tridimensionale degli abitanti
del cerchio?
Immaginiamo che nello spazio euclideo ci sia un'enorme sfera
dipinta all'interno di nero, con un raggio lunghissimo, miliardi
di anni-luce, in modo da contenere tutto l'universo conosciuto.
Immaginiamo di vivere vicino al centro e di essere molto piccoli
rispetto alla sfera all'interno della quale i regoli di misura
si contraggono e i raggi di luce deviano esattamente come
abbiamo descritto per C.
Queste ipotesi sono perfettamente compatibili con la nostra
esperienza.. Se fossero vere, lo spazio intorno a noi sarebbe
iperbolico!
|
| |
|
 |
 |
|
|