|
Geometria iperbolica > I modelli della geometria iperbolica>
Poincaré
|
Il modello
di Poincaré consiste nel seguente "dizionario":
|
| Termini
primitivi
|
Interpretazione |
| Punto
|
Punto interno ad
un cerchio fissato C nel
piano euclideo |
| Linea
|
Parte interna a C
di una linea euclidea |
| Linea retta
|
Parte interna a C
di un diametro di C o di un
cerchio ortogonale a C |
| Piano
|
Interno del cerchio
C |
| Punto su
una retta
|
Punto che appartiene in senso euclideo
alla retta |
| Punto tra
due punti di una retta
|
Punto tra i due punti della retta |
| Lunghezza
di un segmento AB
|
|log (ABUV)| (*)
dove U e V sono i punti di C
che si trovano sulla retta passante per
A e B |
| Ampiezza
di un angolo
|
Ampiezza in radianti dell'angolo euclideo
tra le semirette lati dell'angolo (**)
|
| Segmenti
congruenti
|
Segmenti di uguale lunghezza |
| Angoli congruenti
|
Angoli di uguale ampiezza |
|
| (*)
In questa espressione compare il birapporto;
|
DEFINIZIONE |
| |
Il
birapporto di quattro punti allineati A, B, C, D, che
indichiamo (ABCD), è definito mediante la seguente
espressione: |
(ABCD)
= AC BD / AD BC |
| dove AC, AD, BC, BD
denotano segmenti orientati. |
Questa definizione può
essere estesa, con opportune modifiche, anche a punti non
allineati, come possono essere quelli appartenenti ad una
conica.
Nel birapporto
(ABUV) i segmenti sono intesi nel senso euclideo.
|
| |
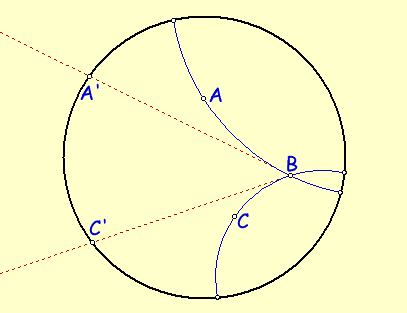
(**)
Dati tre punti A, B,
e C, la misura dell'angolo ^ABC che ha per
lati le linee AB e BC (semirette per gli
abitanti di C) è uguale a
quella dell'angolo euclideo ^A'B'C' dove A'B'
e B'C' sono tangenti in B alle linee precedenti.
 |
| |
Tramite
questa interpretazione i postulati della geometria iperbolica
diventano teoremi della geometria euclidea, e per questo motivo
ogni contraddizione eventualmente deducibile dai postulati
iperbolici potrebbe essere tradotta, ricorrendo a questo "dizionario",
in una contraddizione deducibile dai teoremi euclidei corrispondenti.
Ma poiché la nostra ipotesi è che non vi siano
contraddizioni nella geometria euclidea, non ve ne saranno
nemmeno in quella iperbolica.
Possiamo concludere che la geometria iperbolica è coerente
solo se lo è quella euclidea.
Vale anche il viceversa: la geometria euclidea è coerente
solo se lo è quella iperbolica, quindi l'affermazione
diventa più forte, e ci permette di stabilire una perfetta
equivalenza delle due geometrie rispetto al requisito di non
contraddittorietà.
|
Riflettiamo
ancora:
cosa possiamo rispondere alla secolare questione del V postulato,
e cioè se il V postulato sia deducibile dalla geometria
neutrale?
|
| Se
la geometria euclidea è coerente, la risposta è
no!
|
Se infatti il V postulato
fosse deducibile dalla geometria neutrale, allora sarebbe un
teorema della geometria iperbolica. Ma in questo modo sarebbe
in contraddizione con il POSTULATO 1 e quindi la geometria iperbolica
non sarebbe coerente. Ma abbiamo appena visto che se la geometria
euclidea è coerente, allora lo è anche quella
iperbolica, quindi
se la geometria euclidea è coerente, il V postulato non
può essere dedotto dalla geometria neutrale.
[Più semplicemente, se il V postulato fosse conseguenza
logica degli altri postulati, ovvero della geometria neutrale,
ogni insieme di enti che soddisfa tali proposizioni dovrebbe
soddisfare anche il V postulato. Ma abbiamo appena visto che
gli enti del modello di Poincarè soddisfano tutti gli
altri assiomi e non il V postulato.] |
| |
|
 |
 |
|
|