|
Geometria iperbolica > I modelli della geometria iperbolica>
Poincaré
|
Torniamo
agli abitanti di C.
Essi non si renderanno
conto di vivere all'interno di un cerchio: per quante volte
riportino consecutivamente un metro lungo quello che noi sappiamo
essere un diametro del cerchio, non raggiungeranno mai il
bordo, perché il metro si accorcia troppo velocemente.
Vicino al bordo la lunghezza di un regolo, così come
ogni altra lunghezza, si avvicina al valore |
| |
| Per ricoprire
la distanza che li separa dal bordo, di regoli infinitesimi,
ma per loro sempre uguali, ne occorreranno sempre più.
Dunque, per coloro che vivono al suo interno, il cerchio C
si estende all'infinito in tutte le direzioni, e costituisce
il "piano".
Gli abitanti di C
intenderanno per "linea retta" il percorso di un
raggio di luce (come probabilmente fece Euclide), o il percorso
più breve tra due punti (come Archimede), e poiché
all'interno di C queste due nozioni
sono equivalenti, in ogni caso, le linee rette sono per loro
quelle che noi vediamo come parti interne di diametri di C
o di archi di circonferenze ortogonali a C.
Le rette infinite saranno quindi i diametri, esclusi gli estremi,
e gli archi di cerchi ortogonali, esclusi i punti di intersezione
con C.
|
Siccome i raggi di luce all'interno
di C seguono esattamente questi
percorsi, ciascuna linea disegnata in azzurro in figura
apparirà rettilinea ad un osservatore che guardi
lungo di essa.
|
|
|
|
| Gli abitanti di questo strano
mondo accetteranno il POSTULATO
1, osserviamo infatti per esempio la figura |
| 
|
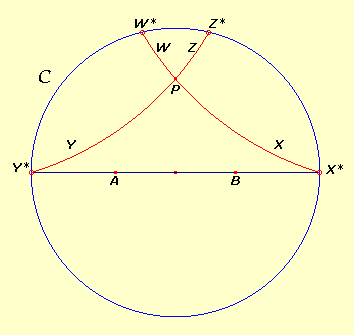
| in cui A e
B giacciono su un diametro, le parallele asintotiche
ad AB per P saranno due archi di cerchio ortogonali
YPZ e WPX passanti per gli estremi Y*
e X* del diametro (osserviamo che questi punti stanno
su C, dunque per gli abitanti non
esistono, per loro il cerchio non ha bordo). Le parallele divergenti
saranno gli archi di cerchio che uniscono P ai punti
su C compresi fra Y* e W*,
mentre le rette non parallele saranno gli archi ortogonali (e
un diametro) che uniscono P ai punti su C
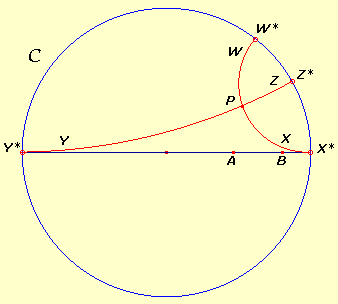
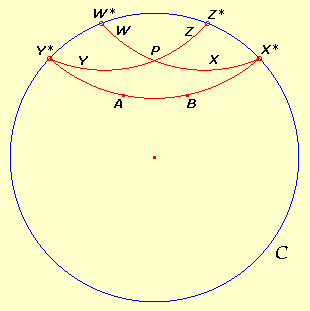
compresi fra W* e Z*. Anche
quando A e B non sono in posizione simmetrica
rispetto al centro di C, o quando non giacciono su
un diametro, la situazione è analoga.
|
  |
| |
 |
 |
|
|