Geometria iperbolica > Teoremi e definizioni > Introduzione
|
Il postulato
iperbolico
|
| Trattando la
questione delle rette parallele abbiamo visto una negazione
del postulato di Playfair; da qui in poi svilupperemo la geometria
iperbolica sulla base di una versione più forte della
negazione di tale postulato.
|
| 
|
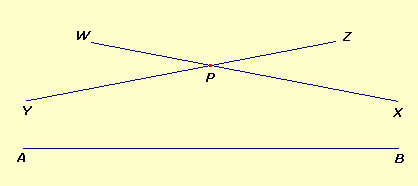
POSTULATO 1
Se P è un punto qualunque e AB una retta
qualunque che non passa per P (nemmeno se prolungata),
allora vi sono due rette YPZ e WPX passanti per P
tali che:
i) YPX non è un'unica retta,
ii) YPZ e WPX sono entrambe parallele ad AB,
iii) nessuna retta passante per P interna a ^YPX è
parallela ad AB. |
|
| La
condizione i) afferma semplicemente che YPZ e WPX
sono rette distinte.
Questo postulato comprende la negazione del postulato di Playfair
vista in precedenza, e in più due ulteriori affermazioni.
Innanzitutto asserisce che l'esistenza di parallele multiple
è un fenomeno universale che si verifica per ogni punto
P del piano e per ogni retta AB non passante
per esso. mentre il postulato di Playfair garantiva che questo
accadesse almeno una volta, per un punto ed una retta particolari.
Inoltre le due parallele del postulato 1 sono le due parallele
più basse, in ambo le direzioni, passanti per P;
la condizione iii) afferma infatti che una retta per P al
di sotto di una delle due non sarebbe parallela ad AB.
Questa proprietà non era specificata per le parallele
del postulato di Playfair.
|
| |
I termini
primitivi della geometria iperbolica sono gli stessi che intervengono
nella geometria euclidea: punto, linea retta, superficie e
superficie piana.
Anche gli altri termini vengono mantenuti, con l'aggiunta
di nuovi che definiremo via via.
Gli assiomi sono le nozioni comuni euclidee e tutti i postulati
eccetto il V, che viene sostituito dal POSTULATO 1.
Questo fa sì che restino validi tutti i teoremi della
geometria neutrale, e cioè i teoremi che si possono
dimostrare senza l'utilizzo del V postulato.
Inizieremo quindi la conoscenza della geometria iperbolica
osservando soprattutto gli aspetti in cui diverge dalla geometria
euclidea.
|
| |
|
Credo che
nella conoscenza di nuovi oggetti geometrici non si possa
prescindere dai principali teoremi che li coinvolgono, nella
trattazione che segue ne presenterò perciò diversi,
della maggior parte di essi però fornirò solo
l'enunciato e qualche breve osservazione affinché la
trattazione risulti il più possibile divulgativa. Per
conoscerne le dimostrazioni ed approfondire in generale l'argomento
suggerisco alcuni dei testi elencati nella bibliografia: vedi
libri e siti consigliati. |
| |
 |
 |