|
Geometria iperbolica > Teoremi e definizioni > Introduzione
|
Introduzione
alla geometria iperbolica
|
| Uno dei postulati
logicamente equivalenti al V è quello di Playfair,
quindi una buona negazione del V può essere formulata
come la negazione del postulato di Playfair.
Ovvero: |
| |
Esistono
almeno un punto P ed una retta AB tali che
i) P non è su AB né sul suo prolungamento
ii) per P passano almeno 2 rette parallele ad AB
|
|
|
Accettiamo la geometria neutrale e
sostituiamo il V postulato con questo, saremo allora in una
geometria non euclidea: quella iperbolica.
Come è possibile che vi siano due parallele alla stessa
retta passanti per lo stesso punto?
|
Siamo abituati a pensare che, data
AB ed il punto P, ci sia solo la retta CD
come parallela alla prima.
|
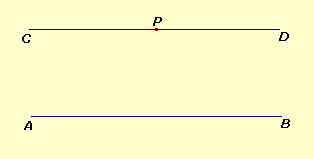
fig.1
|
Ma proviamo a pensare
che ne esista una seconda: pensiamo ad una retta passante per
P che non coincida con CD. |
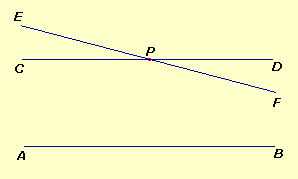 fig.2
fig.2 |
Diremmo
che questa non possa essere parallela ad AB perché
convinti che incontri AB in un certo punto prima o poi. Ma
proviamo a prescindere dall'apparenza del disegno; possiamo
dimostrare che il prolungamento di EF debba per forza
incontrare AB?
Teniamo presente che siamo in una geometria neutrale a cui
abbiamo aggiunto la negazione del postulato di Playfair, non
abbiamo più il teorema 30 di Euclide che ci dice che
rette parallele ad una stessa retta sono parallele fra loro,
quindi non deve disturbarci il fatto che nel nostro caso EF
e CD, entrambe parallele ad AB, si incontrino
in P.
|
E ancora, non abbiamo più il
postulato di Euclide che ci porterebbe a dire che, poiché
PQB+QPF<180°,
le due rette AB e EF si incontrano.
|
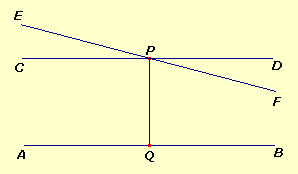
fig.3 |
E potremmo andare avanti ancora, scontrandoci
con asserzioni logicamente equivalenti al V postulato, e trovandoci
a dover ogni volta ricordare che l'abbiamo negato.
La verità è che nel disegno sembra talmente
evidente che EF incontrerà AB che
crediamo di poterlo dimostrare, ma significherebbe dimostrare
che AB è l'unica parallela, ovvero dimostrare
il postulato euclideo, problema che è stato spina nel
fianco dei matematici per 2000 anni!
Ai nostri occhi può sembrare che la negazione del postulato
di Playfair sia "incompatibile con la natura di una linea
retta", per dirla alla Saccheri, ma dobbiamo sforzarci
di superare ed ingannare il consueto modo di pensare la geometria
e non spaventarci dal fatto che la geometria iperbolica sfugge
da ogni tentativo di rappresentazione intuitiva.
Proviamo a passare da un sistema assiomatico materiale, o teoria
scientifica, a un sistema assiomatico formale.
E convinciamoci che un sistema matematico (sistema assiomatico
formale) è sostanzialmente una pura struttura logica,
alla quale si può annettere un significato o meno.
Forse in questo modo la geometria iperbolica ci disarmerà
un po' meno.
Proviamo per un attimo a credere che
le rette CD e EF siano entrambe parallele
ad AB senza pretendere che questo abbia il significato
che siamo soliti attribuire alla geometria che descrive il
nostro mondo fisico.
|
| Disegniamo
in questo modo le nostre rette: |
|
fig.4
|
Ora forse è più facile
credere che EF non necessariamente incontrerà
AB.
Del resto possiamo accettare questo disegno poiché la
geometria iperbolica è un sistema assiomatico formale
e "linea retta" è un termine non definito e
non possiamo realmente sapere come si comporti quando la prolunghiamo.
Di EF sappiamo che è parallela ad AB e che
non la incontrerà, effettivamente l'ultimo disegno
tiene conto di questo e non ci costringe a dubitare.
N.B. Con il disegno
di fig.4 non intendo dire che nella geometria iperbolica le
linee rette si incurvano.
In realtà non sappiamo ancora come si comportino; "linea
retta" è semplicemente un'espressione per indicare
uno dei tipi di oggetti di cui la geometria iperbolica si occupa.
E' importante capire che fig.4 offre una rappresentazione non
meno valida di fig.2.
Per conoscere alcune rappresentazioni della geometria iperbolica
si vedano i suoi principali modelli.
|
 |
 |