|
Geometria iperbolica > I modelli della geometria iperbolica>
Poincaré
|
Supponiamo
infine che il fenomeno che caratterizza C
costringa ai raggi di luce che si propagano tra due punti
interni al cerchio a seguire sempre il percorso più
breve, se misurato nel sistema di misura degli abitanti di
C.
Al nostro punto di vista, un raggio di luce che unisce due
punti sarà dritto solo se i due punti sono su un diametro
di C; altrimenti presenterà
una convessità rivolta verso il centro, poiché
i regoli di misura si allungano andando in quella direzione.
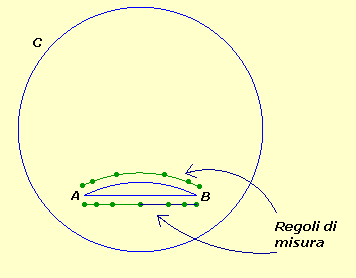
Osserviamo la figura |
| 
|
| Il
percorso rettilineo da A a B misura 6 metri,
il percorso curvilineo invece ne misura 5, questo avviene
perché il regolo si allunga avvicinandosi al centro,
e per ricoprire il percorso curvilineo ne occorre uno in meno.
|
E' possibile dimostrare
che questi cammini curvi sono archi di circonferenze "ortogonali"
a C, cioè archi di circonferenze
che incontrano C in modo tale che
nei punti di intersezione le rispettive tangenti siano perpendicolari
fra loro.
|
| 
|
Dunque nello strano mondo descritto
i raggi di luce si propagheranno lungo i diametri di C
e lungo archi interni a C appartenenti
a circonferenze ortogonali a C. |
| |
|
 |
 |