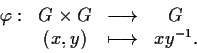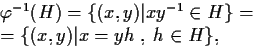- a)
- se
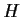 è
aperto,
è
aperto, 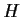 è anche chiuso;
è anche chiuso;
- b)
- se
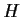 è chiuso e
è chiuso e
![$[G:H]$](img3.gif) è finito,
è finito, 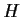 è anche aperto;
è anche aperto;
- c)
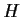 è
aperto se e solo se
è
aperto se e solo se
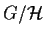 è discreto.
è discreto.
- a), b)
- Sia
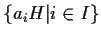 l'insieme dei laterali sinistri di
l'insieme dei laterali sinistri di 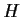 in
in 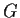 distinti, che costituiscono
una partizione di
distinti, che costituiscono
una partizione di 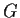 :
:
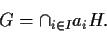
Allora, se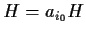 ,
,
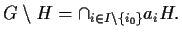
Se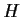 è aperto,
è aperto,
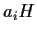 è aperto
è aperto
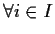 ;
allora
;
allora
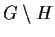 è aperto e
dunque
è aperto e
dunque 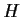 è chiuso.
è chiuso.
Se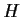 è chiuso e
è chiuso e 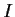 è un insieme finito,
è un insieme finito,
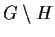 è chiuso e quindi
è chiuso e quindi 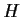 è aperto.
è aperto.
- c)
-
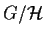 è discreto se e solo se
è discreto se e solo se ![$\{[a]\}$](img13.gif) è
aperto in
è
aperto in
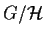 ,
,
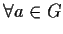 ,
cioè se e solo se
,
cioè se e solo se 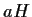 è
aperto in
è
aperto in 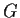 ,
,
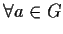 ,
cioè se e solo se
,
cioè se e solo se 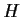 è aperto in
è aperto in 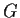 .
.