Definizione 1
Sia
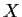
uno spazio topologico e sia
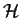
un sottogruppo di
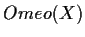
.
Diremo che
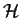
è un
gruppo d'omeomorfismi che agisce su
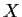
.
Due elementi
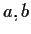
di
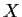
si dicono equivalenti se esiste un omeomorfismo
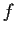
di
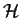
per cui
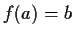
.
Questa è una relazione di equivalenza su
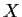
.
Chiamiamo
orbita di
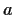
la classe di equivalenza di
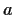
,
cioè
l'insieme
![$[a]=\{f(a)\vert f\in \mathcal{H}\}$](img8.gif)
,
e denotiamo con
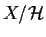
lo spazio topologico
quoziente.
Proposizione 2
Sia
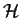
un gruppo
d'omeomorfismi che agisce su uno spazio topologico
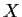
;
allora la proiezione
canonica
è aperta.
Dimostrazione
Sia 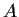 un aperto
di
un aperto
di 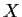 .
Allora
.
Allora
è un aperto di
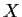
essendo
unione di aperti (
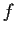
è un omeomorfismo). Pertanto
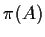
è aperto in
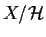
.
Proposizione 3
Sia
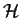
un gruppo d'omeomorfismi che agisce su uno spazio topologico
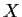
.
Se l'insieme
è chiuso in
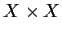
,
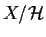
è
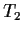
.
Dimostrazione
Segue
immediatamente dal fatto che se 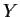 è uno spazio topologico, la diagonale
è chiusa in
è uno spazio topologico, la diagonale
è chiusa in 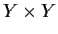 se e solo se
se e solo se 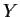 è
è 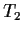 .
.
![\begin{displaymath}\begin{array}{cccc} \pi:&X&\longrightarrow&X/\mathcal{H}\\
&a&\longmapsto&[a]\end{array}\end{displaymath}](img10.gif)
![]() un aperto
di
un aperto
di ![]() .
Allora
.
Allora ![\begin{eqnarraystar}\pi^{-1}(\pi(A))&=&\{a\in X\vert[a]\in
\pi(A)\}=\\ &=&\cup_{...
...p_{f\in
\mathcal{H}}\{f(a)\}=\\ &=&\cup_{f\in \mathcal{H}}f(A)\end{eqnarraystar}](img12.gif)
![]() è uno spazio topologico, la diagonale
è chiusa in
è uno spazio topologico, la diagonale
è chiusa in ![]() se e solo se
se e solo se ![]() è
è ![]() .
.