Dimostrazione
Unicità. Se esiste una tale topologia, questa è unica in
quanto
![]() ,
il sistema degli intorni di
,
il sistema degli intorni di ![]() è necessariamente
è necessariamente
![]() .
.
Esistenza. Sia
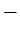
- Verifichiamo che
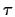 è una topologia su
è una topologia su 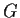 :
:
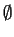 ,
,
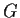 appartengono a
appartengono a 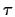 ;
;
- se
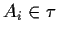 ,
,
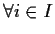 ,
,
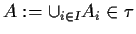 ;
infatti
;
infatti
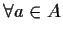 ,
,
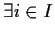 tale che
tale che
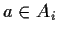 ;
allora
;
allora
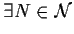 per cui
per cui
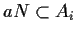 e dunque
e dunque
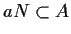 .
.
- se
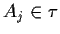 con
con
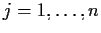 ,
,
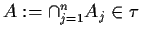 ;
infatti
;
infatti
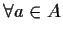 ,
,
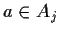 ,
,
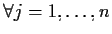 ;
allora
;
allora
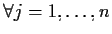 ,
,
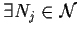 tale che
tale che
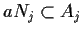 .
Quindi se
.
Quindi se
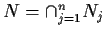 ,
,
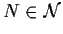 per la proporietà
per la proporietà 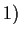 ,
e
,
e
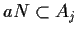
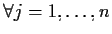 ,
cioè
,
cioè
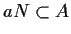 .
.
- Proviamo ora che
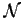 è il sistema degli intorni di
è il sistema degli intorni di 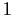 per la topologia
per la topologia 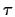 .
.
- Ogni
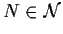 è intorno di
è intorno di 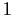 ;
infatti:
;
infatti:
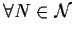 sia
sia
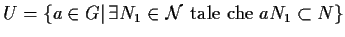 .
.
Dalla definizione di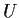 segue:
segue:
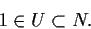
Proviamo che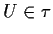 .
Sia
.
Sia 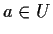 ;
esiste
;
esiste
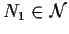 tale che
tale che
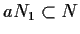 .
Dalla proprietà
.
Dalla proprietà 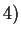 segue che
esiste
segue che
esiste
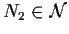 per cui
per cui
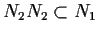 ;
quindi
;
quindi
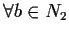 ,
,
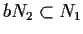 ,
cioè
,
cioè
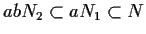 .
Allora
.
Allora 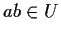
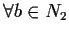 ,
cioè
,
cioè
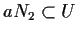 .
Dunque
.
Dunque
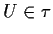 .
.
- Ogni intorno
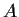 di
di 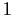 appartiene a
appartiene a
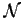 ;
infatti:
;
infatti:
per ipotesi esiste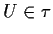 tale che
tale che
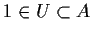 .
Allora
.
Allora
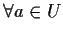 esiste
esiste
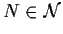 tale che
tale che
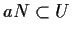 ,
quindi in
particolare
,
quindi in
particolare
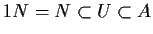 .
Dalla proprietà
.
Dalla proprietà 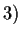 segue allora che
segue allora che
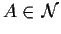 .
.
- Ogni
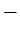
- Proviamo che per ogni
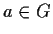 ,
,
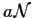 è il sistema degli intorni di
è il sistema degli intorni di 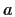 .
.
-
Facciamo vedere che
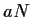 è intorno di
è intorno di 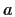 ,
,
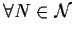 :
sia
:
sia
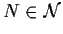 ;
esiste
;
esiste 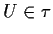 tale che
tale che
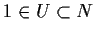 .
Allora
.
Allora
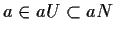 ,
e
,
e 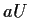 è un aperto di
è un aperto di 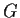 ;
infatti ogni elemento di
;
infatti ogni elemento di
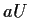 è della forma
è della forma 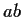 con
con 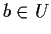 ,
ed esiste
,
ed esiste
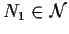 tale
che
tale
che
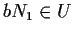 ,
cioè
,
cioè
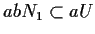 .
.
- Viceversa se
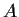 è
un intorno di
è
un intorno di 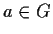 ,
,
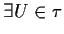 tale che
tale che
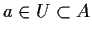 .
.
Allora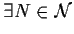 per cui
per cui
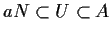 ,
quindi
,
quindi
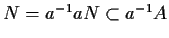 da cui per la proprietà
da cui per la proprietà 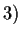 si ha
si ha
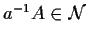 ,
cioè
,
cioè
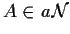 .
.
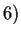 segue che anche
segue che anche
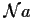 è il sistema degli intorni di
è il sistema degli intorni di 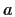 ,
cioè
,
cioè
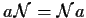 .
Infatti
.
Infatti
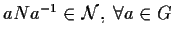 ,
quindi
,
quindi
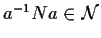 ,
quindi
,
quindi
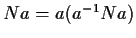 è intorno di
è intorno di 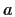 ,
e ogni intorno di
,
e ogni intorno di 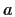 ,
,
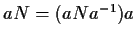 è della forma
è della forma 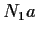 con
con
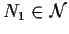 .
.
-
Facciamo vedere che
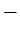
- Rimane da
provare che
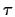 è compatibile con la struttura di gruppo di
è compatibile con la struttura di gruppo di 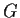 :
:
consideriamo l'applicazione
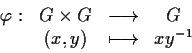
e proviamo che è continua.
Se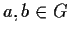 ,
ogni intorno di
,
ogni intorno di 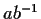 è della forma
è della forma
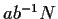 con
con
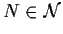 .
Per la proprietà
.
Per la proprietà 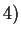
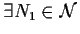 tale che
tale che
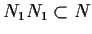 ,
e per la proprietà
,
e per la proprietà 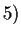
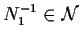 ;
inoltre, esiste
;
inoltre, esiste
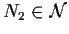 tale che
tale che
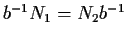 .
.
Allora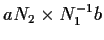 è un
intorno di
è un
intorno di 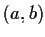 in
in 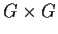 tale che
tale che
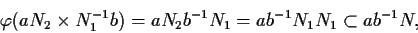
cioè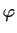 è continua in
è continua in 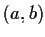 per ogni
per ogni
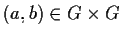 .
.
