- 1)
- se
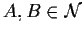 allora
allora
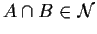 ;
;
- 2)
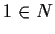 ,
,
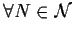 ;
;
- 3)
- se
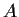 è un insieme contenente un intorno di
è un insieme contenente un intorno di 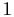 ,
anche
,
anche 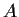 è un intorno di
è un intorno di 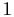 ;
;
- 4)
-
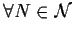 ,
,
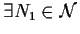 tale che
tale che
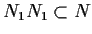 ;
;
- 5)
-
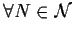 ,
,
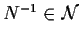 ;
;
- 6)
-
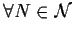 ,
,
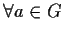 ,
,
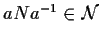 .
.
Le proprietà 1), 2), 3) sono un'immediata conseguenza della definizione di intorno di un punto.
- 4)
- L'applicazione
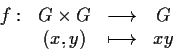
è continua, quindi, poichè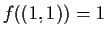 ,
,
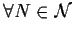
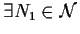 tale che
tale che
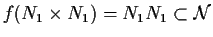 .
.
- 5)
- L'applicazione
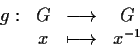
è un omeomorfismo tale che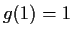 .
Allora
.
Allora
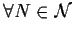 ,
,
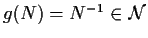 .
.
- 6)
- Se
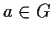 ,
anche l'applicazione
,
anche l'applicazione
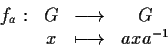
è un omeomorfismo (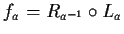 )
che lascia fisso
)
che lascia fisso 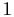 .
Quindi
.
Quindi
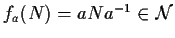 ,
,
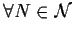 .
.
