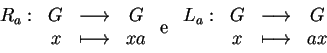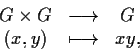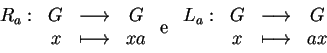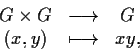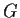
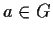
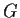
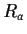
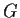
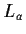
Proposizione 1   Sia $G$un gruppo topologico. Per ogni $a\in G$, la traslazione destra di $G$, $R_{a}$, e la traslazione sinistra di $G$, $L_{a}$, sono degli omeomorfismi.

Dimostrazione

\begin{displaymath}\begin{array}{cccc}R_{a}:& G&\longrightarrow& G\\ &x&\longmap... ...ccc}L_{a}:& G&\longrightarrow& G\\ &x&\longmapsto&ax\end{array}\end{displaymath}

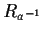
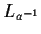
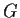
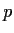
sono biunivoche con inversa $R_{a^{-1}}$ e $L_{a^{-1}}$ rispettivamente, e sono bicontinue essendo $G$ un gruppo topologico. Infatti detta $p$ l'applicazione prodotto

\begin{displaymath}\begin{array}{ccc} G\times G&\longrightarrow&G\\ (x,y)&\longmapsto&xy,\end{array}\end{displaymath}

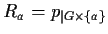
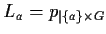
si ha $R_{a}=p_{\vert G\times \{a\}}$ e $L_{a}=p_{\vert\{a\}\times G}$.

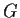
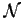
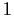
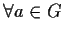
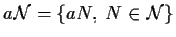
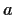
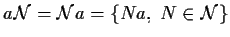
Corollario 2   Sia $G$ un gruppo topologico. Se $\mathcal{N}$ è il sistema degli intorni dell'elemento neutro $1$, $\forall a \in G$ la famiglia $a\mathcal{N}=\{aN,\;N\in \mathcal{N}\}$ è il sistema degli intorni di $a$. Inoltre $a\mathcal{N}=\mathcal{N}a=\{Na,\;N\in \mathcal{N}\}$.

Dimostrazione
Segue dalla proposizione 1 osservando che

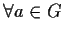
\begin{displaymath}L_{a}(N)=aN \quad e \quad R_{a}(N)=Na\end{displaymath}

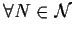
$\forall a \in G$ e $\forall N\in \mathcal{N}$.

Notazione 3   Se $A$ e $B$ sono sottoinsiemi di un gruppo $G$, poniamo:
$AB=\{ab,\;a\in A,\,b\in B\},$
$A^{-1}=\{a^{-1},\;a\in A\}.$


previousup next