Definizione-Proposizione 2
Sia
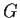
un gruppo. Per ogni
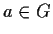
denotiamo con
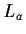
la
traslazione sinistra di
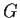
definita da
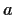
,
cioè l'applicazione
e con
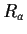
la
traslazione destra di
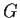
definita da
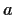
,
cioè l'applicazione
Gli insiemi
sono sottogruppi di
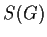
e quindi sono gruppi di trasformazione.
Dimostrazione
Vediamolo per
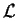 :
:
- proviamo innanzi tutto che
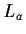 è biunivoca:
è biunivoca: 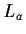 è iniettiva in quanto se
è iniettiva in quanto se
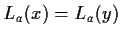 ,
cioè se
,
cioè se 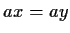 ,
per la legge di cancellazione in
,
per la legge di cancellazione in 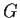 si ha
si ha 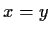 ;
per provare la suriettività di
;
per provare la suriettività di 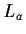 ,
consideriamo un elemento
,
consideriamo un elemento 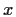 di
di 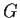 .
Possiamo scrivere
.
Possiamo scrivere
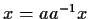 ,
cioè
,
cioè
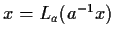 .
.
- proviamo ora che
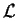 è un sottogruppo di
è un sottogruppo di 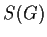 :
:
In modo analogo si prova che
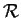
è un gruppo di
trasformazioni.
Teorema 3 (
di
Cayley)
Ogni gruppo è isomorfo a un gruppo di trasformazioni.
Dimostrazione
Sia 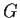 un gruppo.
Proviamo che
un gruppo.
Proviamo che
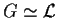 ,
dove
,
dove
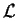 è il gruppo
delle traslazioni a sinistra di
è il gruppo
delle traslazioni a sinistra di 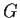 .
Consideriamo l'applicazione
.
Consideriamo l'applicazione
La
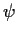
è un omomorfismo in quanto
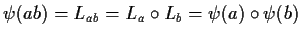
,
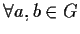
,
è ovviamente
suriettiva, ed è iniettiva essendo
Corollario 4
Sia
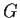
un gruppo finito di ordine
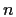
;
allora
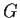
è isomorfo a un
sottogruppo di
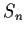
,
il gruppo simmetrico su
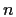
lettere.
Dimostrazione
Segue dal teorema 3, osservando che
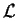 è un sottogruppo di
è un sottogruppo di
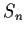 .
.
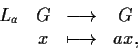
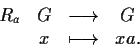
![]() :
:
![]() un gruppo.
Proviamo che
un gruppo.
Proviamo che
![]() ,
dove
,
dove
![]() è il gruppo
delle traslazioni a sinistra di
è il gruppo
delle traslazioni a sinistra di ![]() .
Consideriamo l'applicazione
.
Consideriamo l'applicazione 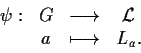
![]() è un sottogruppo di
è un sottogruppo di
![]() .
.