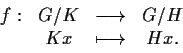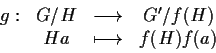Teorema 1
Siano
un gruppo,
un sottogruppo normale di
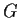
,
e
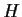
un
sottogruppo di
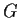
contenente
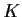
;
allora
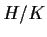
è un sottogruppo
di
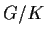
.
Inoltre, se
e
esiste una corrispondenza biunivoca
Infine
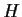
è normale in
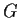
se e solo se
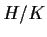
è normale in
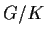
.
In
questo caso si ha
Dimostrazione
Osserviamo che essendo
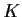
normale in
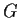
,
è normale anche in
ogni sottogruppo
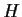
di
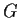
che lo contiene, quindi possiamo usare la
notazione
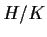
.
Per
proposizione 3 della sezione "Omomorfismi di gruppi", applicata alla proiezione
canonica
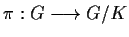
si ha che
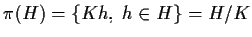
è un sottogruppo di
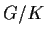
.
Inoltre, se
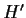
è un
sottogruppo di
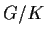
,
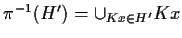
è un
sottogruppo di
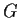
che contiene
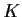
,
e si ha
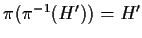
essendo
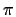
suriettiva; quindi
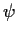
è suriettiva.
Inoltre
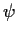
è iniettiva: siano
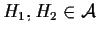
,
tali che
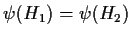
,
cioè
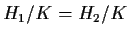
.
Allora
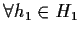
,
esiste un
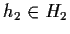
tale
che
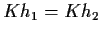
.
Ciò implica
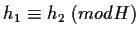
,
cioè
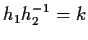
,
con
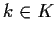
.
Allora
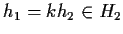
.
Abbiamo in questo modo provato che
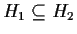
;
in modo analogo si verifica che
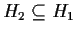
e
quindi si ha
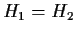
.
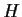 è normale in
è normale in 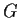 se e solo se
se e solo se 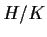 è normale in
è normale in 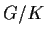 :
:
se 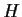 è normale,
è normale,
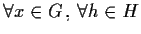 ,
,
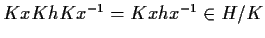 ,
poiché
,
poiché
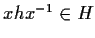 .
Viceversa se
.
Viceversa se 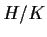 è normale in
è normale in 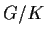 ,
,
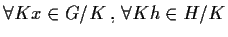 ,
,
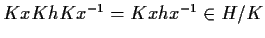 ,
cioè
,
cioè
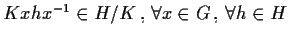 .
Allora
.
Allora
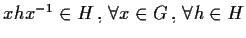 .
.
Se 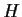 è normale,
è normale,
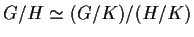 :
consideriamo
l'applicazione
:
consideriamo
l'applicazione
L'applicazione
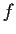
è ben definita; infatti se
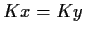
,
con
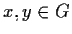
,
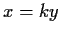
,
con
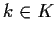
.
Allora
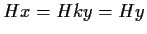
,
poiché
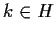
.
Inoltre
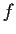
è un omomorfismo
in
quanto
ed è ovviamente suriettiva.
Poiché
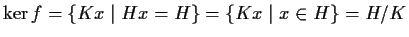
,
per il
teorema fondamentale di omomorfismo si ha
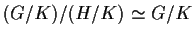
.
Teorema 2
Sia
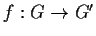
un omomorfismo di gruppi suriettivo, e sia
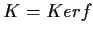
.
Allora esiste una corrispondenza biunivoca
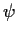
tra
l'insieme dei sottogruppi di
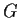
contenenti
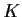
e l'insieme dei
sottogruppi di
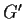
,
definita da
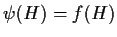
.
Inoltre
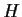
è
normale in
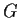
se e solo se
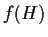
è normale in
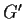
;
in questo
caso l'applicazione
è un
isomorfismo.
Dimostrazione
Segue da
corollario 2 della sezione "Teorema fondamentale di omomorfismo di gruppi", e da
teorema 1.
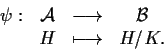
![]() è normale in
è normale in ![]() se e solo se
se e solo se ![]() è normale in
è normale in ![]() :
:
![]() è normale,
è normale,
![]() ,
,
![]() ,
poiché
,
poiché
![]() .
Viceversa se
.
Viceversa se ![]() è normale in
è normale in ![]() ,
,
![]() ,
,
![]() ,
cioè
,
cioè
![]() .
Allora
.
Allora
![]() .
.
![]() è normale,
è normale,
![]() :
consideriamo
l'applicazione
:
consideriamo
l'applicazione