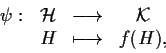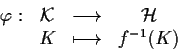Proposizione 10
Siano
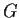
e
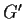
due gruppi isomorfi, e sia
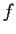
un isomorfismo tra
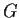
e
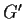
.
Allora:
- 1)
- per ogni
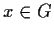 ,
,
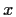 e
e 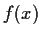 hanno lo stesso
ordine;
hanno lo stesso
ordine;
- 2)
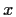 è un generatore per
è un generatore per 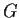 se e solo se
se e solo se 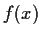 è un
generatore per
è un
generatore per 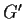 .
In particolare
.
In particolare 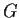 è ciclico se e solo se lo
è
è ciclico se e solo se lo
è 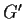 ;
;
- 3)
- se
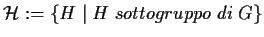 e
e
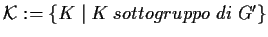 ,
esiste una
corrispondenza biunivoca
,
esiste una
corrispondenza biunivoca
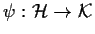 tale che
tale che
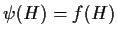 .
.
Inoltre, se 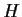 è un sottogruppo di
è un sottogruppo di 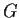 ,
,
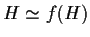 .
.
Dimostrazione
Siano
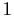
e
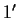
gli elementi neutri di
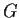
e
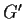
rispettivamente.
- 1)
- Per ogni
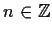 ,
per ogni
,
per ogni 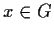 ,
si ha:
,
si ha:
quindi 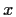 e
e 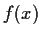 hanno lo stesso periodo.
hanno lo stesso periodo.
- 2)
- Sia
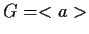 ;
;
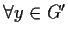 ,
esiste
,
esiste 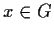 ,
con
,
con 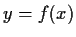 ;
quindi esiste
;
quindi esiste
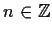 ,
con
,
con 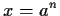 ,
cioè
,
cioè
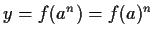 ,
cioè
,
cioè
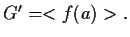 Il viceversa è analogo.
Il viceversa è analogo.
- 3)
- Le applicazioni
sono ben definite per
proposizione 3 della sezione "Omomorfismi di gruppi". Inoltre
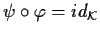 e
e
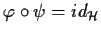 per la biunivocità di
per la biunivocità di 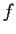 ,
quindi
,
quindi 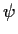 è biettiva.
è biettiva.
Per finire, se 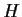 è un
sottogruppo di
è un
sottogruppo di 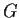 ,
l'applicazione
,
l'applicazione
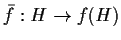 tale che
tale che
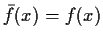 è un isomorfismo di gruppi.
è un isomorfismo di gruppi.
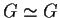 ;
;
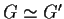 ,
allora
,
allora
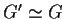 ;
;
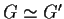 e
e
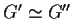 ,
allora
,
allora
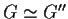 .
.
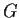 è un
isomorfismo di
è un
isomorfismo di 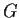 in
in
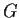 ,
quindi
,
quindi 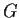 è isomorfo a se stesso.
è isomorfo a se stesso.
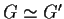 ,
esiste un
isomorfismo
,
esiste un
isomorfismo
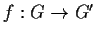 .
Allora
.
Allora
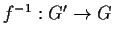 è un
isomorfismo, e quindi
è un
isomorfismo, e quindi
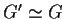 .
.
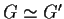 e
e
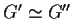 ,
esistono due
isomorfismi
,
esistono due
isomorfismi
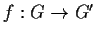 e
e
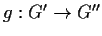 .
L'applicazione
.
L'applicazione 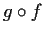 è allora un isomorfismo di
è allora un isomorfismo di 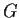 in
in
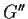 .
.