Esempio 4
Se
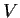
è uno spazio vettoriale euclideo di dimensione
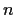
,
i
gruppi
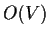
e
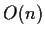
sono isomorfi.
Infatti, poiché
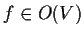
se e solo se la matrice di
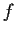
,
rispetto ad una qualsiasi base
ortonormale di
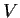
,
è ortogonale, l'applicazione
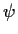
dell'
esempio 2, scelta
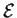
base ortonormale, induce un
isomorfismo di
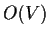
su
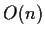
.
Esempio 6
Sia
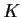
un campo, e sia
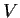
un
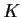
-spazio vettoriale di dimensione
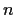
.
Il sottogruppo
di
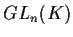
,
è
isomorfo al sottogruppo
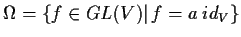
;
infatti l'isomorfismo
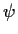
dell'
esempio 2 induce un isomorfismo di
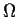
su
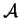
.
Esempio 7
Se
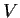
è uno spazio vettoriale hermitiano di dimensione
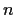
,
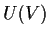
è
isomorfo al gruppo
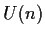
.
Infatti l'isomorfismo
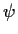
dell'
esempio 2 induce, scelta
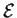
base
ortonormale,
un isomorfismo di
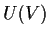
in
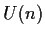
in
quanto
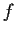
sta in
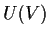
se e solo se la matrice
che la rappresenta rispetto alla base ortonormale
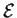
appartiene a
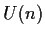
.