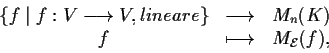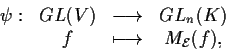Esempio 2
Sia
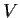
un
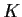
-spazio vettoriale di dimensione
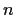
,
e sia
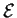
una sua base.
I gruppi
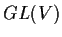
e
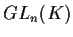
sono
isomorfi.
Infatti, un'applicazione
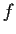
appartiene a
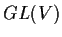
se e
solo se la matrice che la rappresenta rispetto alla base
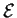
,
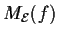
,
è un elemento di
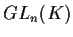
;
allora l'applicazione biunivoca
induce una
corrispondenza biunivoca
che è un isomorfismo: